Liekta renīte PQR nostiprināta virs galda. Mazu lodīti X atbrīvo punktā P. Tā slīd lejup un punktā R saduras ar lodīti Y. Pēc absolūti elastīgas sadursmes lodīte Y uzsāk kustību horizontāli ar ātrumu 3,0 m/s un nokrīt uz grīdas punktā S. Lodītes ir vienādas. Gaisa pretestību un berzi starp lodīti un renīti neievēro! \(g=9,8\space \mathrm{m/s^2}\).
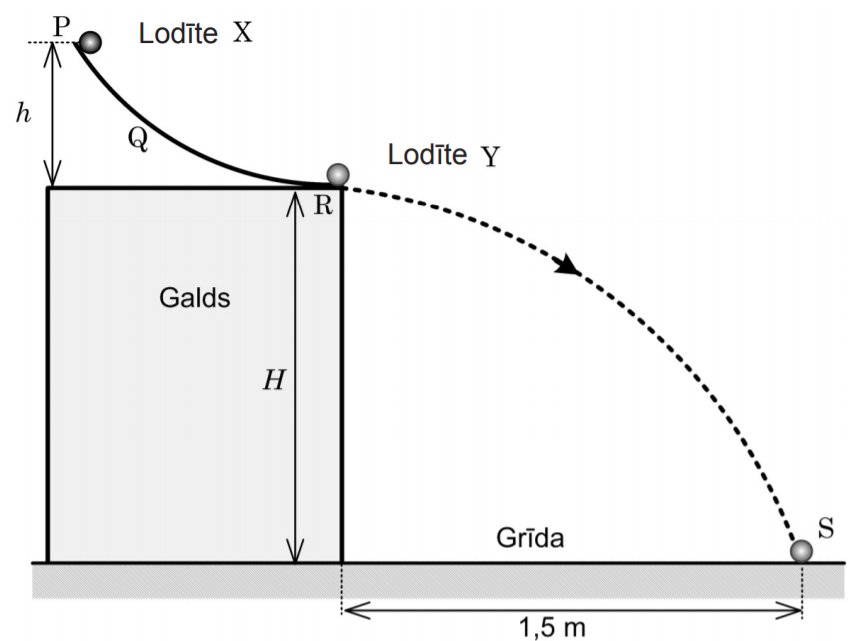
Aprēķini, cik liels ir lodītes X ātrums īsi pirms sadursmes!
Aprēķini, cik liels ir augstums \(h\)!
Aprēķini, cik liels ir augstums \(H\)!
Absolūti elastīgā sadursmē saglabājas gan impulss, gan mehāniskā enerģija. Ja abām lodītēm ir vienāda masa, tad, pēc impulsa nezūdamības likuma, mijiedarbības rezultātā notiek "ātrumu apmaiņa" – lodīte X apstājas, bet lodīte Y uzsāk kustību horizontālā virzienā ar lodītes X ātrumu pirms sadursmēs. Tātad, var secināt, ka pirms sadursmes lodītes X ātrums ir \(3,0\space\mathrm{m/s}\).
Pierādījums:
Apzīmējumi: \(m\) – lodīšu masa, \(v\) – lodītes X ātrums pirms sadursmes, \(u_1\) – lodītes X ātrums pēc sadursmes, \(u_2=3,0\space\mathrm{m/s}\) – lodītes Y ātrums pēc sadursmes. Jāatrisina vienādojumu sistēma atbilstoši impulsa un mehāniskās enerģijas nezūdamības likumiem:
\(\begin{cases} mv-mu_1=mu_2\\ \frac{mv^2}{2}=\frac{mu_1^2}{2}+\frac{mu_2^2}{2} \end{cases}\)
Saīsinot masu un veicot matemātiskus pārveidojumus, iegūst:
\(\begin{cases} v=u_1+u_2 \\ v^2=u_1^2+u_2^2 \end{cases}\)
Ievieto pirmo vienādojumu otrajā un iegūst
\((u_1+u_2)^2=u_1^2+u_2^2\)
\(u_1^2+2u_1u_2+u_2^2=u_1^2+u_2^2 \implies\\u_1u_2=0\)
Ja \(u_2=3,0\space\mathrm{m/s}\), tad \(u_1=0\). No vienādojuma \(v=u_1+u_2\) iegūst, ka \(v=0+3,0=3,0\space\mathrm{m/s}\).
Lodīte X kustas bez berzes, tādēļ ir spēkā mehāniskās enerģijas nezūdamības likums. Punktā P lodītei piemīt tikai potenciālā enerģija \(E_{\mathrm{pot}}=mgh\), punktā R – tikai kinētiskā enerģija \(E_{\mathrm{kin}}=\frac{mv^2}{2}\). Potenciālās enerģijas nulles līmeni izvēlas punktā R augstumā \(H\) no grīdas. Pielīdzinot enerģijas izteiksmes \(mgh=\frac{mv^2}{2}\) , nosaka lodītes X sākuma augstumu: \(h=\frac{v^2}{2g}=\frac{3,0^2}{2\cdot 9,8}\approx0,46\space\mathrm{m}\).
Lodīte Y veic horizontālu sviedienu no augstuma H. Horizontālajā virzienā lodīte lido vienmērīgi. Tādēļ lidojuma laiku \(t\) aprēķina no formulas \(t=\frac{L}{v}\), kur \(L\) – lodītes Y lidojuma tālums horizontālā virzienā (\(L=1,5\space\mathrm m\)), \(v\) – lodītes sākuma ātrums (\(v=3,0\space\mathrm{m/s}\)). Tad \(t=\frac{L}{v}=\frac{1,5}{3,0}=0,50\space\mathrm{s}\).
Vertikālajā virzienā lodīte Y brīvi krīt no augstuma \(H\), jo berzi un gaisa pretestību neņem vērā. Saistību starp augstumu \(H\) un krišanas laiku \(t\) apraksta formula \(H=\frac{gt^2}{2}\space\implies H=\frac{9,8\cdot0,50^2}{2}\approx1,2\space\mathrm m\).
Aprēķini:
Augstums \(h=\frac{v^2}{2g}=\frac{3^2}{2\cdot 9,8}\approx0,46\space\mathrm{m}\).
Lidojuma laiks \(t\) horizontālajā virzienā \(t=\frac{L}{v}=\frac{1,5}{3}=0,50\space\mathrm{s}\).
Augstums \(H=\frac{gt^2}{2}=\frac{9,8\cdot0,50^2}{2}\approx1,2\space\mathrm m\).
Var noteikt H augstumu ar vienu izteiksmi: \(H=\frac{g(\frac{L}{v})^2}{2}=\frac{9,8\cdot(\frac{1,5}{3,0})^2}{2}\approx1,2\space\mathrm m\).
Atbilde: Lodītes sākuma ātrums \(v\) ir \(3,0\space\mathrm{m/s}\), augstums \(h\) ir \(0,46\space\mathrm m\), augstums \(H\) ir \(1,2\space\mathrm m\).
Vērtēšanas kritēriji
Skaidro, kāpēc lodītes X ātrums pirms sadursmes arī ir 3 m/s – 1 punkts.
Izmanto enerģijas nezūdamības likumu lodītes X sākuma augstuma \(h\) noteikšanai – 1 punkts.
Aprēķina lodītes X sākuma augstumu \(h\) – 1 punkts.
Aprēķina lodītes Y lidojuma laiku \(t\) horizontālā virzienā – 1 punkts.
Aprēķina augstumu \(H\). Iegūst augstuma skaitlisko vērtību un pieraksta to ar mērvienībām – 1 punkts.
Skolēnu risinājumu un to vērtējumu piemēri
1. piemērs: risinājums novērtēts ar 5 punktiem.
