Ja ķermeni izvirza no stabila līdzsvara stāvokļa un tas perodiski tajā atgriežās, tad attiecīgo kustību sauc par mehāniskajām svārstībām. Piemēram, ja mēs paņemam dusmīgo putnu un iekaram to atsperē, tad šī sistēma ieņem līdzsvara stāvokli (1. att.). Ja kādā brīdi dusmīgais putns tiek izvirzīts no līdzsvara stāvokļa, tad rodas atgriezējspēks Fat (1. attēls, 2. stāvoklis), kas cenšas dusmīgo putnu nogādāt atpakaļ līdzsvara stāvoklī. Tas arī notiek, bet inerces dēļ dusmīgais putns aiztraucas līdzsvara stāvoklim garām un atkal rodas atgriezējspēks, tikai šoreiz pretējā virzienā (1. attēls, 4. stāvoklis), un tā dusmīgais putns ir sācis svārstīties.
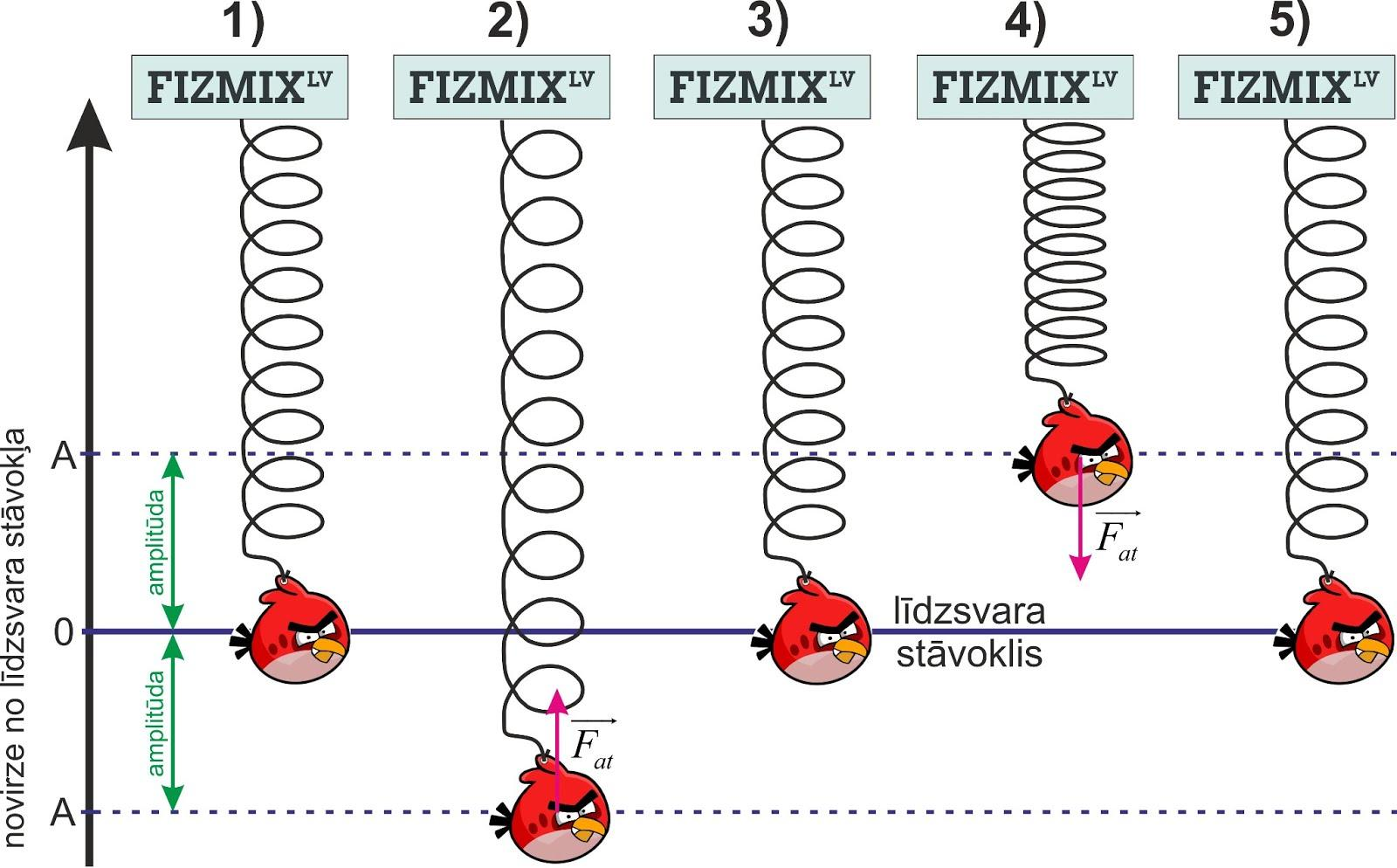
2. att. Svārstību kustība
Svārstības raksturo dažādi raksturlielumi.
Par svārstību periodu T sauc laiku, kādā notiek viena pilna svārstība.
Svārstību frekvence f vienāda ar svārstību skaitu laika vienībā. Ja laika vienība ir sekunde, tad frekvences mērvienība ir Hz. Svārstību periods un frekvence ir apgriezti lielumi: f=1/T un T=1/f. Piemēram, ja frekvence ir 50 Hz, tad, katra svārstība notiek 1:50 sekundēs.
Par svārstību amplitūdu A sauc ķermeņa maksimālo novirzi no līdzsvara stāvokļa.
Ķermenis var svārstīties dažādos veidos, piemēram, to pašu dusmīgo putnu varam iekārt nevis atsperē, bet diegā (2. att.). Arī šādā gadījumā, novirzot dusmīgo putnu no līdzsvar stāvokļa un palaižot vaļā, un to darbojas atgriezējspēks, un dusmīgais putns sāk svārstīties. Šīs svārstības var raksturot ar iepriekš apskatītajiem raksturlielumiem.
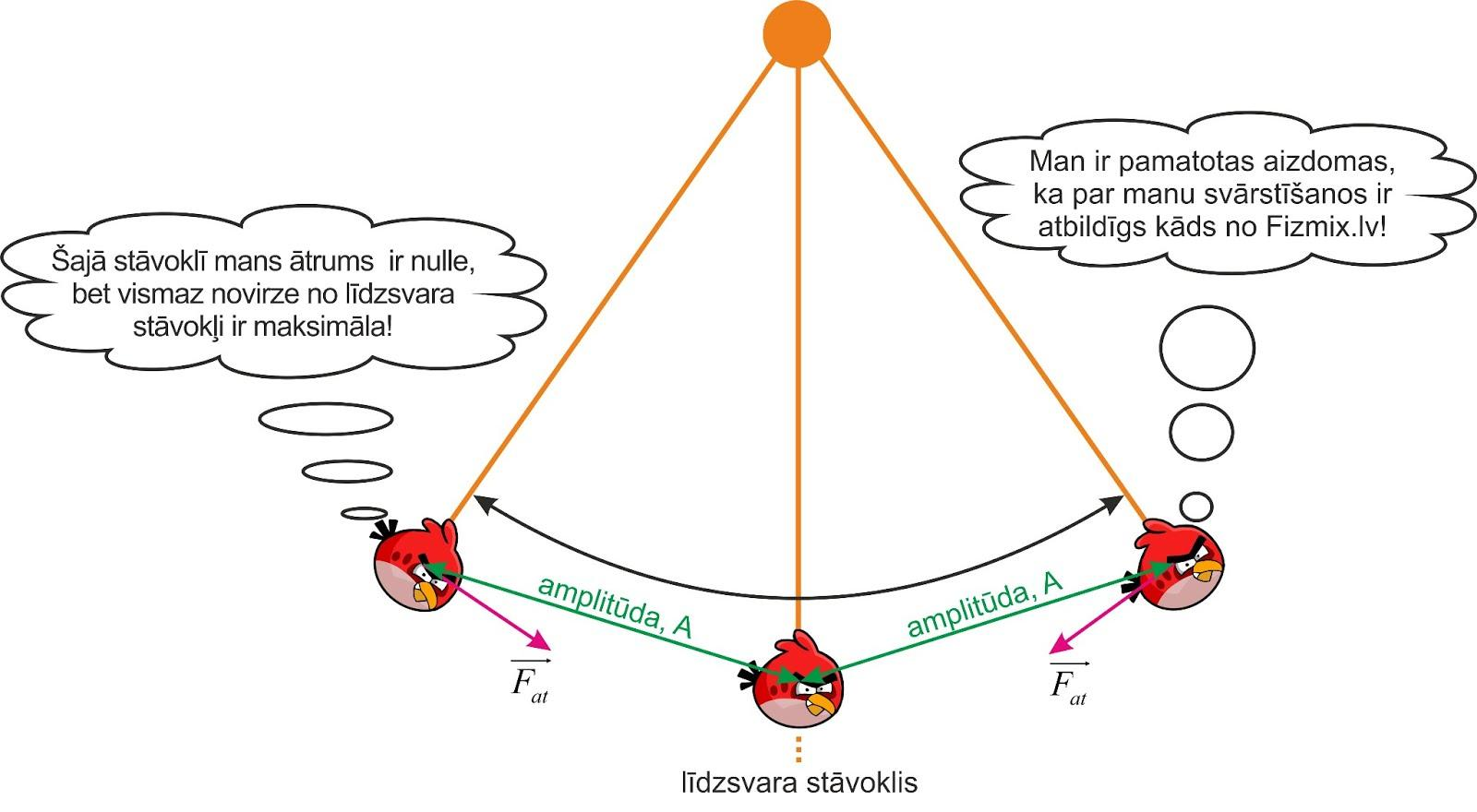
2. att. Svārstību raksturlielumi
Atsperes svārsts sastāv no atsperē vai elastīgā auklā iekārta ķermeņa. Ja ķermeni izvirza no līdzsvara stāvokļa par lielumu ∆x, tad rodas elastības spēks Fe=k∆x, kur k ir atsperes vai auklas stinguma koeficients. Palaižot ķermeni vaļā, elastības spēks darbojas kā atgriezeniskais spēks, kas cenšas ķermeni nogādāt atpakaļ līdzsvara stāvoklī, līdz ar to nodrošinot atsperes svārsta kustību (1. att.). Svārstības notiek ar periodu, kas atkarīgs no iekārtā ķermeņa masas un stinguma koeficienta (3. att.).
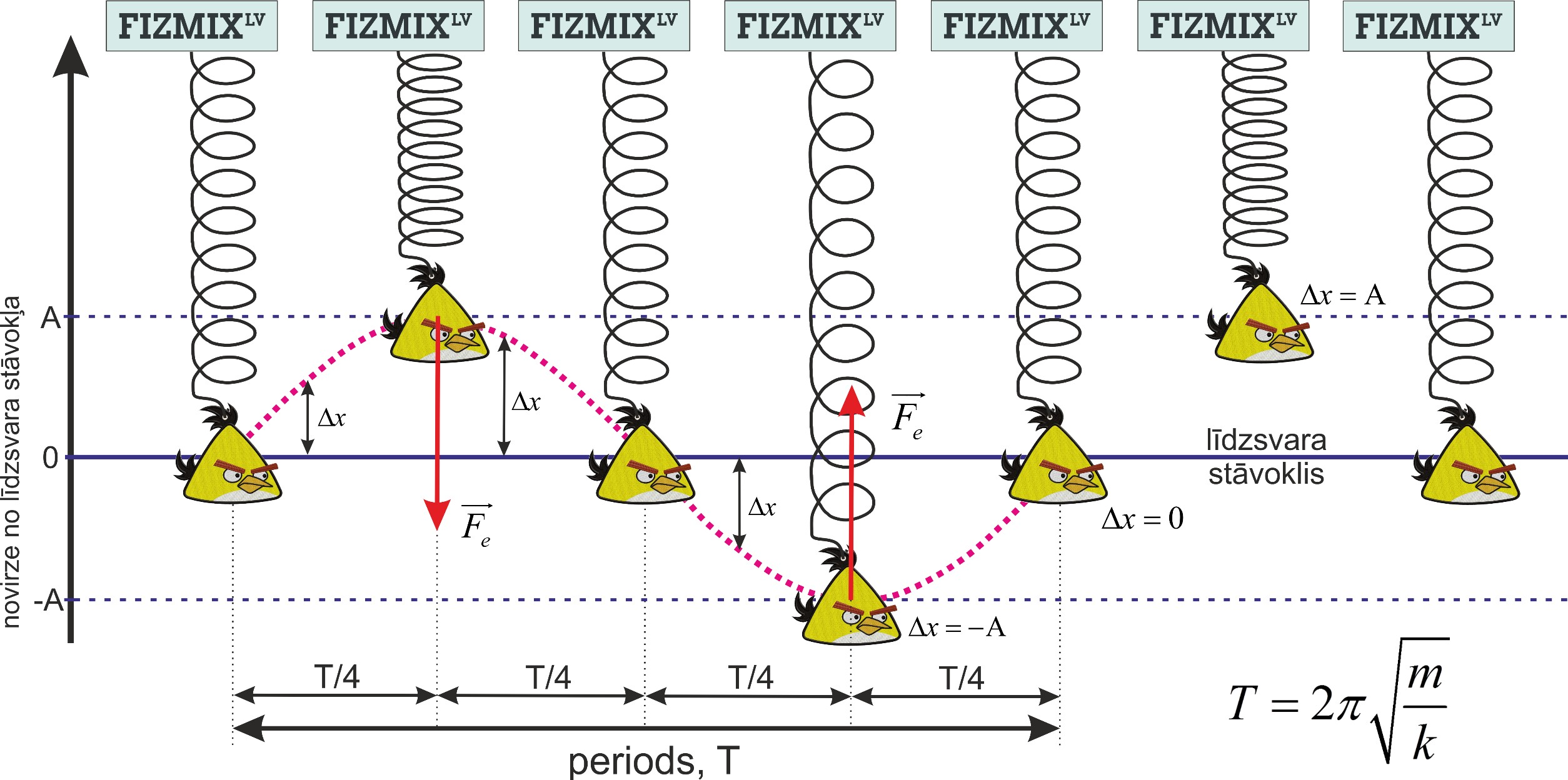
3. att. Atsperes svārsta kustība
Ja tievā diegā vai auklā iekar ķermeni, turklāt, diega vai auklas masa ir niecīga un ķermeni var uzskatīt par masas punktu, tad šādu objektu sauc par matemātisko svārstu. Ja diegā iekārto ķermeni izvirza no līdzsvara stāvokļa par leņķi α, tad rodas nekompensēts smaguma spēks Fat=mgsinα, kur
m - ķermeņa masa, kg
g - ir brīvās krišanas paātrinājums, m/s2
Smaguma spēks, palaižot ķermeni vaļā, darbojas kā atgriezeniskais spēks, kas noteic svārsta kustību (4. att.). Svārstības notiek ar periodu, kas atkarīgs no svārsta garuma l un brīvās krišanas paātrinājuma (4. att.).
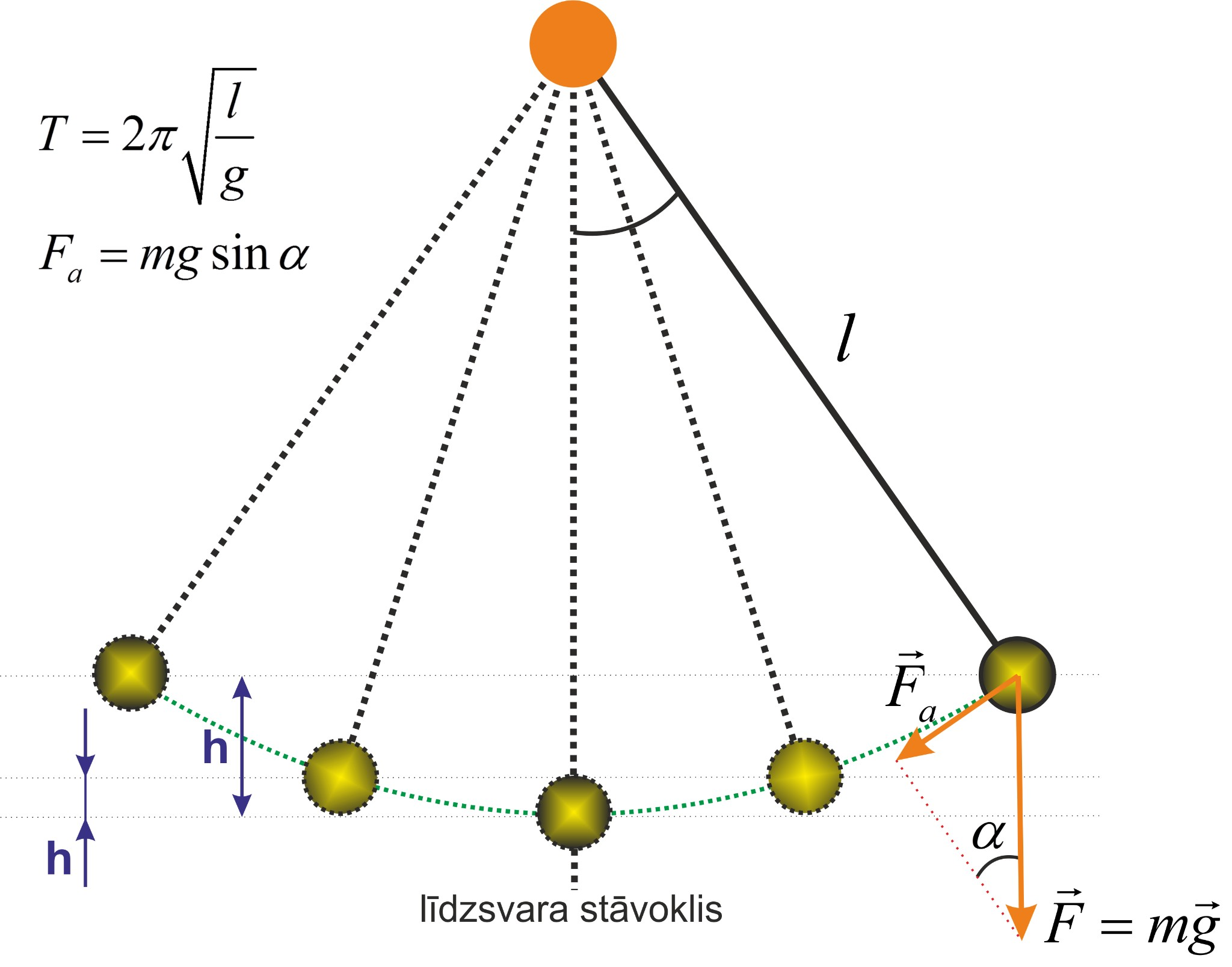
4. att. Matemātiskā svārsta kustība
Ja svārstību kustību attēlo grafiski uz y ass atliekot novirzi no līdzsvara stāvokļa, bet uz x ass laiku, tad iegūst, piemēram, 1. attēla redzamo ainu. Ja svārstība norisinās pēc sinusa vai kosinusa likuma, tad tādas svārstības sauc par harmoniskām svārstībām. Šādas svārstības var aprakstīt ar svārstību vienādojumu, kur
x - novirze no līdzsvara stāvokļa, m
T - periods, s
t - laika moments. s
Lielumu ω sauc par ciklisko frekvenci un aprēķina ω=π/T!
1. att. Ķermeņa svārstības
Svārsta kustības laikā mainās gan ātrums, gan paātrinājums, turklāt harmoniskām svārstībām abi šie lielumi mainās sinosoidāli (2. att.). Ātrums sasniedz savu maksimālo vērtību vmax \(= { \sqrt{k/mA}}\) līdzsvara stāvoklī, savukārt maksimālais paātrinājums amax=kA/m ir tad, kad svārsts atrodas maksimāli novirzīts no līdzsvara stāvokļa.
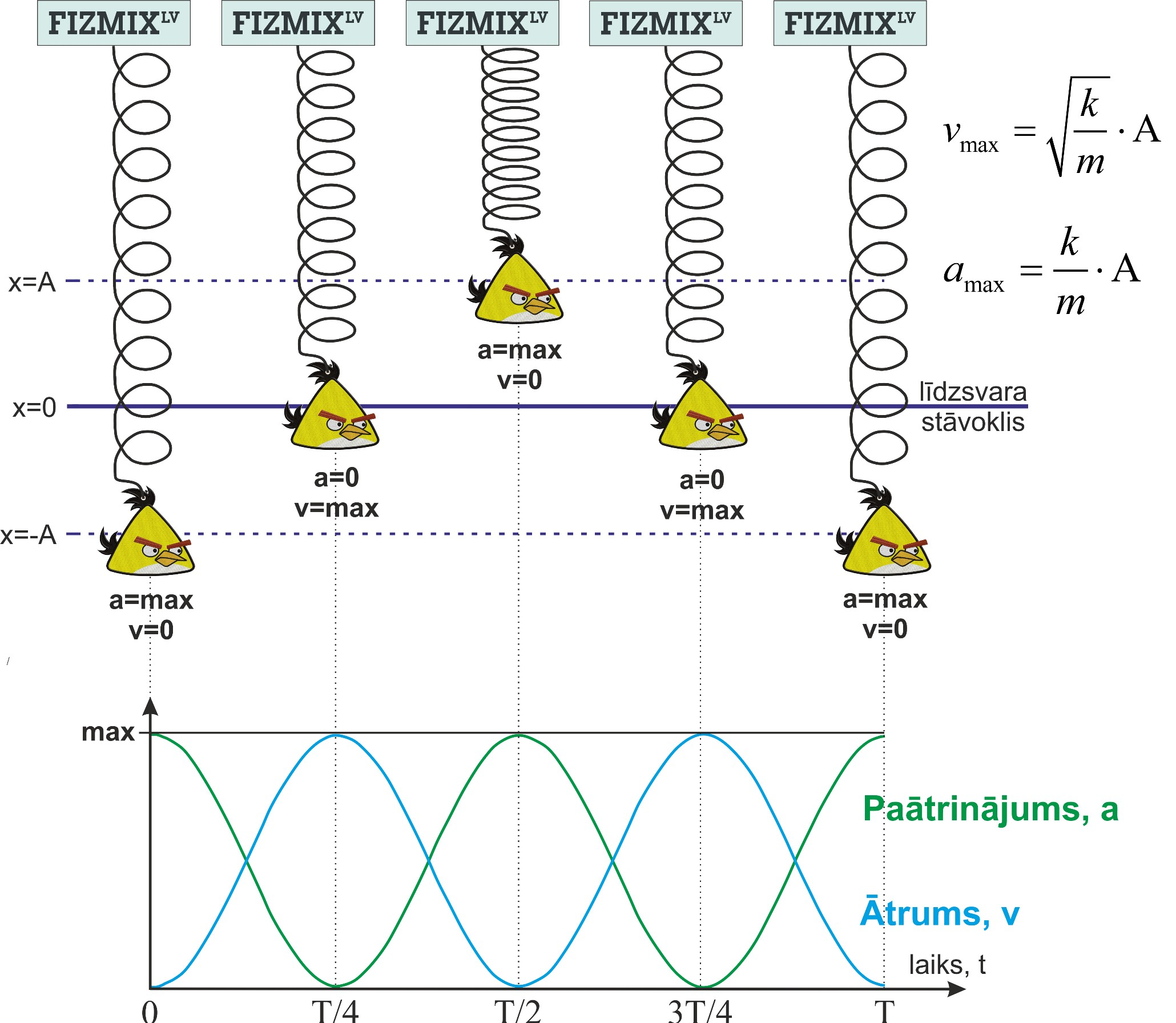
2. att. Atsperes svārsta ātrums un paātrinājums
Atsperes svārstam periodiski mainās ne tikai ātrums un paātrinājums, bet arī kinētsikā un potenciālā enerģija (3. att.). Ja zināma svārsta masa m un ātrums v, tad kinētiskā enerģija Ek=mv2/2. Ja ir zināma svārsta novirze no līdzsvara stāvokļa ∆x un atsperes stinguma koeficients k, tad potenciālo enerģija Ep=kx2/2. Svārstību laikā ir spēka enerģija saglabāšanās likums, tādēļ kopēja enerģija Ekop=Ek+Ep paliek nemainīga. Kopēja enerģija ir vienāda ar maksimālo potenciālo enerģiju jeb potenciālo enerģiju stāvoklī, kad svārstam ir maksimāla novirze no līdzsvara stāvokļa Ekop=kA2/2.
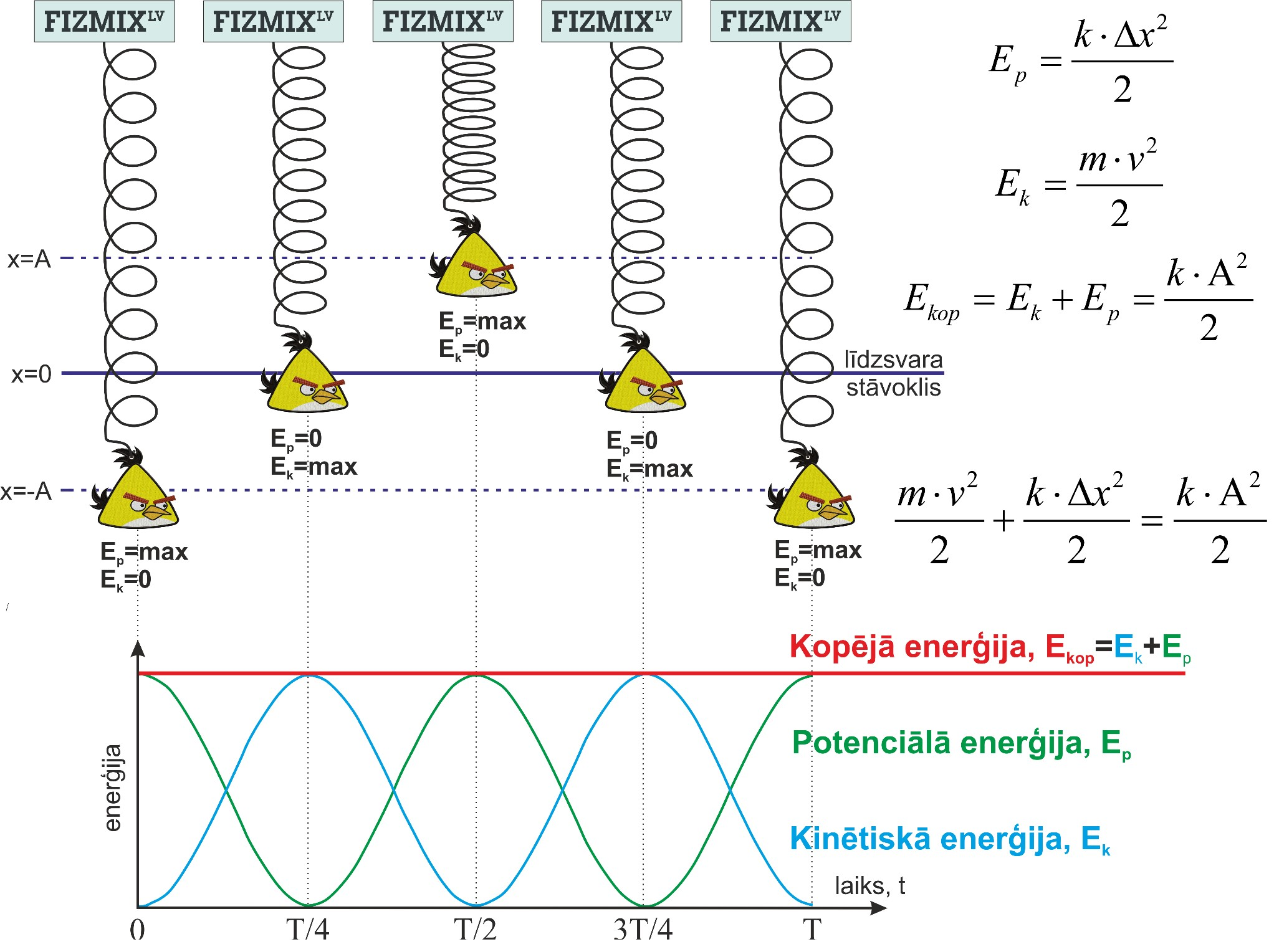
3. att. Atsperes svārsta enerģija
Atsperes svārsta mehānismu var izmantot dažādos tehnoloģiskos risinājumos, piemēram, automašīnas amortizācijas sistēmā, tomēr pastāv iespējas to izmantot arī izklaidējošos nolūkos, piemēram, 4. att. redzama viena no bērnu zinātnes centra Zinoo atrakcijām, kurā bērni var iejusties atsperes svārsta ādā.

4. att. Atsperes svārsts izmantošana Zinoo atrakcijā
Līdzīgi kā atsperes svārsta gadījumā, matemātiskā svārsta kustības laikā mainās gan ātrums, gan paātrinājums (5. att.). Ātrums sasniedz savu maksimālo vertību vmax=\(= { \sqrt{gl}}\)αmax līdzsvara stāvoklī, bet maksimālais paātrinājums ir kāda no galējiem stāvokļiem, kad novirze leņķis ir maksimāls.
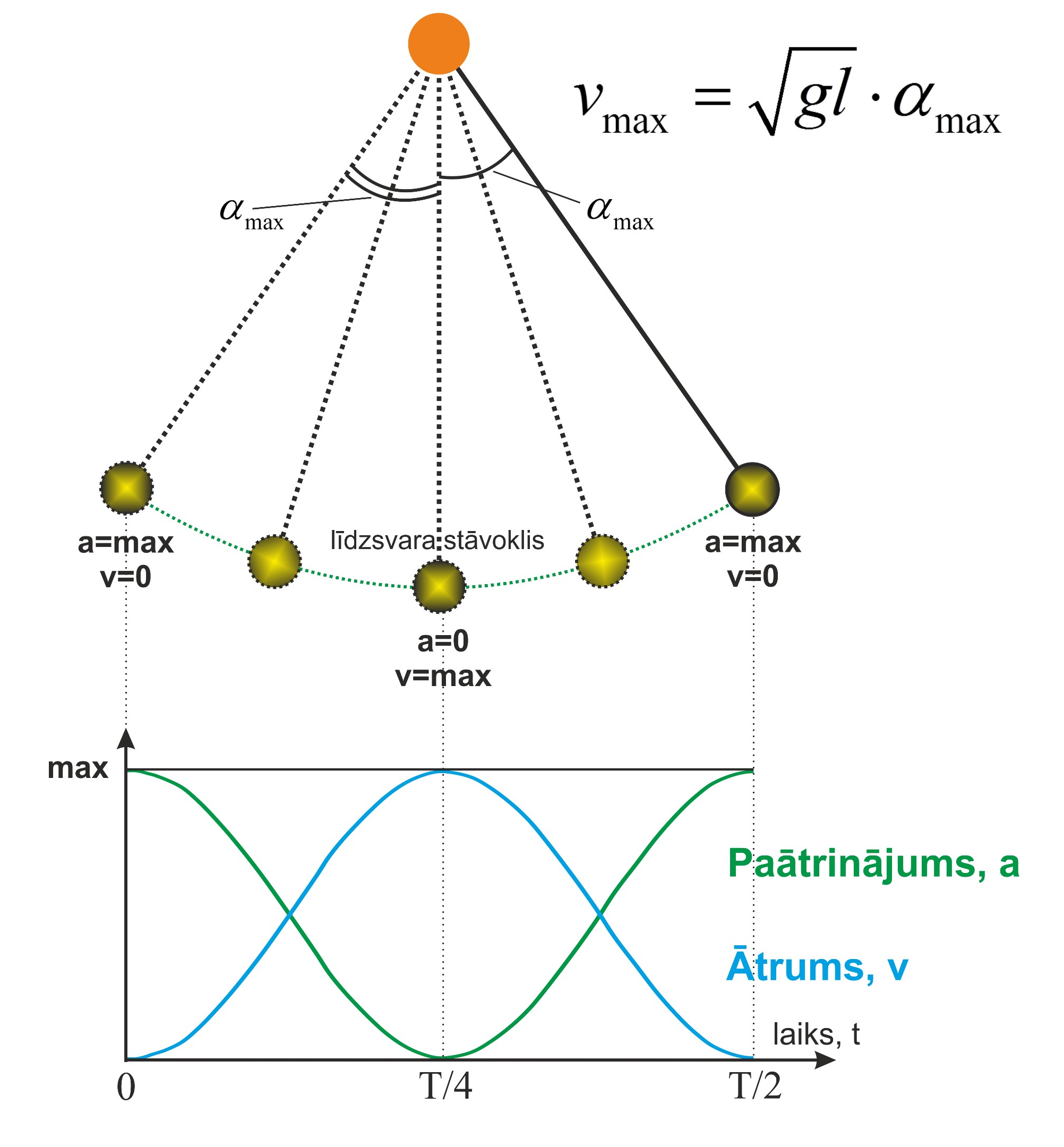
5. att. Matemātiskā svārsta ātrums un paātrinājums
Arī diega svārstam kopēja enerģija Ekop=Ek+Ep svārstību laikā nemainās, bet tās sadale starp kinētisko un potenciālo enerģiju mainās periodiski (6. att.). Svārsta kinētisko enerģiju nosaka piekārtā ķermeņa masa m un ātrums v, proti, Ek=mv2/2. bet potenciālo enerģiju nosaka pēc izteiksmes Ep=mgh, kur h ir piekārtā ķermeņa augstums, salīdzinot ar līdzsvara stāvokli. Kopēja enerģija, līdzīgi kā atsperes svārsta gadījumā, ir vienāda ar maksimālo potenciālo enerģiju, kas realizējas maksimālās novirzes gadījumā no līdzsvara stāvokļa Ekop=mghmax.
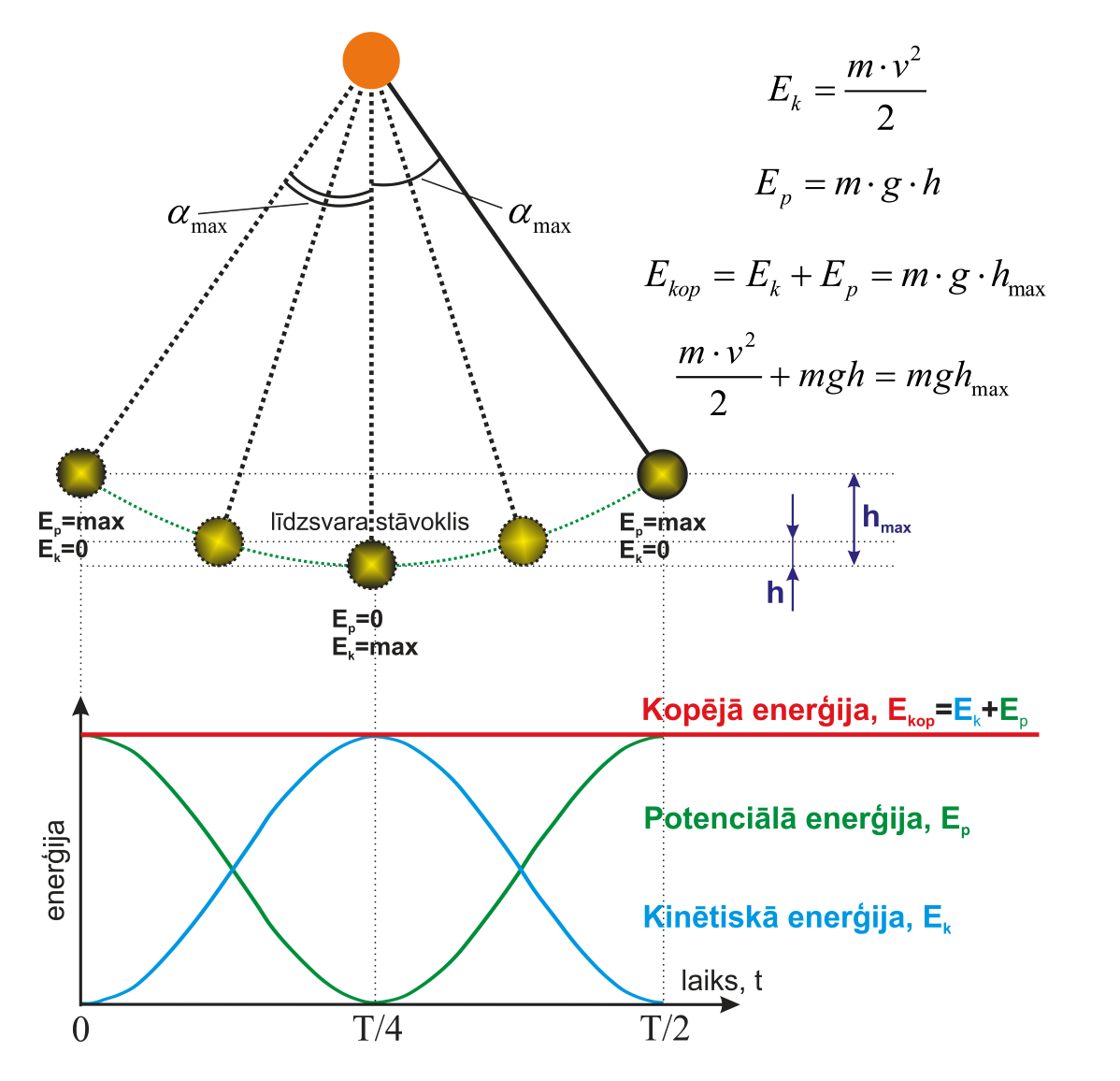
6. att. Matemātiskā svārsta enerģija
Matemātiskos svārstus ar noteiku periodu T ilgu laiku izmantoja pulksteņa konstrukcijās, lai nodrošinātu laika skaitīšanu. Arī dažādu vaida šūpoļu (7. att.) konstrukciju kustība atbilst matemātiskā svārsta principiem.

7.att. Matemātiskā svārsta izmantošana Zinoo atrakcijā
Svārstības ar laiku norimst. Ja rimstošām svārstībām vēlas saglabāt svārstību amplitūdu, tad svārstam ir jāpievada enerģija. Tas iespējams, pievadot periodiski mainīgu ārējo spēku. Šāda veida svārstības sauc par uzspiestajā svārstībām. Piemēram, dažkārt cilvēkiem patīk pārbaudīt dažādu transporta līdzekļu amortizācijas sistēmu, lekājot pat to (8. att.). Pēc viena leciena transporta līdzeklis nosvārstās, bet šīs svārstības ātri norimst, ja vēlās transporta līdzekli šādi iesvārstīt uz ilgāku laiku, tad jālec ir nēpārtraukti, periodiski pievadot sistēmai enerģiju. Šādā gadījumā var teikt, ka transporta līdzeklis ir pakļauts uzspiestajām svārstībām.
8. att. Uzspiestas svārstības
Rezonansei var būt noderīga, piemēram, mikroviļņu krānīs tiek izmantota rezonanse starp mikroviļņiem un ūdens molekulu svārstību pašfrekvenci, lai uzsildītu ēdienu (9. att.).

9. att. Mikroviļņu krāsns
Par harmoniskām svārstībām sauc svārstības, kuras var aprakstīt ar sinosuīdu (1. att.). Sinosuīda ir gan sin, gan cos funkcija. (Sīklietotne par sinosuīdām) Šādām svārstībām ir raksturīga nemainīga svārstību amplitūda atkarībā no laika, kā arī periodiskums. Par harmoniskām svārstībām var uzskatīt svārstības, kas noris ar mazām svārstību amplitūdām un tās tiek apskatītas pietiekoši īsu laika sprīdi, lai svārstību apmlitūda nepaspētu manāmi norimt.
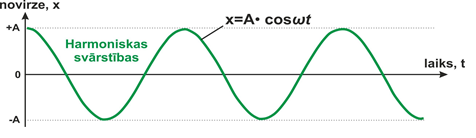
1. att. Harmoniskas svārstības
Svārstības sauc par anharmoniskām, ja tās nevar aprasktīt ar sinosuīdu (2.att.). Šādām svārstībām nav rakstūrīga kāda noteikta svārstību amplitūda un nav periodiskuma, tādēļ šāda svārstību attīstību ir grūti prognozēt. Anharmoniski svārstās, piemēram, atomi dažādas veida molekulās, kā arī metāliska ķermeņa matemātiskais svārsts, kas kustas virs kāda magnēta.
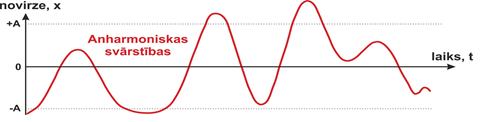
2. att. Anharmoniskas svārstības
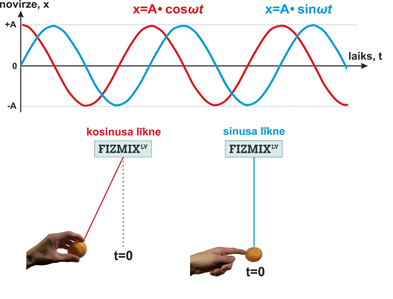
Gan sinusa, gan kosinusa funkcijām ir sinosuidāls raksturs, tādēļ tās abas var lietot harmonisku svārstību aprakstam. Konkrētās funkcijas izvēle ir atkarīga no svārstību sākuma stāvokļa (3. att.)
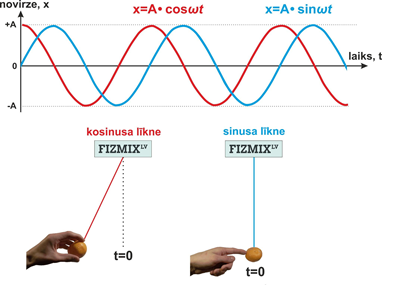
3. att. Svārstību aprakstīšana ar sinusa un kosinusa līkni
Dažādām harmoniskajām svārstībām, piemēram, ar atšķirīgu frekvenci (4. att. a) ir raksturīga nemainīga svārstību amplitūda, jo saglabājās svārstību enerģija. Tomēr reāliem svārstiem enerģija ar laiku tiek zaudēta berzes spēku dēļ, tādēļ svārstību amplitūda samazinās (4. att. b). Šo parādību sauc par svārstību rimšanu.
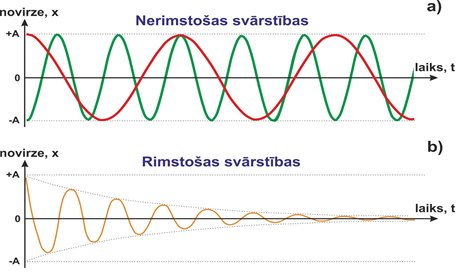
4. att. Nerimstošas un rimstošas svārstības
Lai panāktu, ka rimstošas svārstības neapastājās, svārstībām ir jāpievada enerģija, izmantojot uzspiedējspēku, Uzspiedējspēkam var būt noteikta frekvence, kas nosaka uzspiesto svārstību frekvenci. Tomēr katram svārstam, atkarībā no uzbūves, ir raksturīga sava pašfrekvence, kurā tas “labprāt” svārstītos, ja tam būtu pietiekoši enerģijas. Ja uzspiedējspēka frekvence tuvojas svārsta pašsvārstību frekvencei, tad ir novērojams straujš svārstību amplitūdas pieaugums (5. att.) To sauc par svārstību rezonansi.
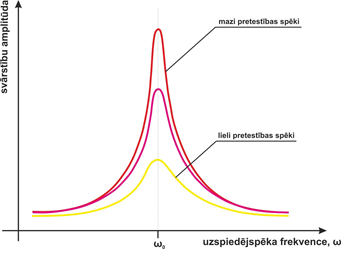
5. att. Amplitūdas maiņa atkarībā no uzspiedējspēka frekvences