Vasarā zēni nolēma izklaidēties, lecot ūdenskrātuvē. Viņi izveidoja svārstu, kas karājās pāri ūdenskrātuves ūdens virsai.
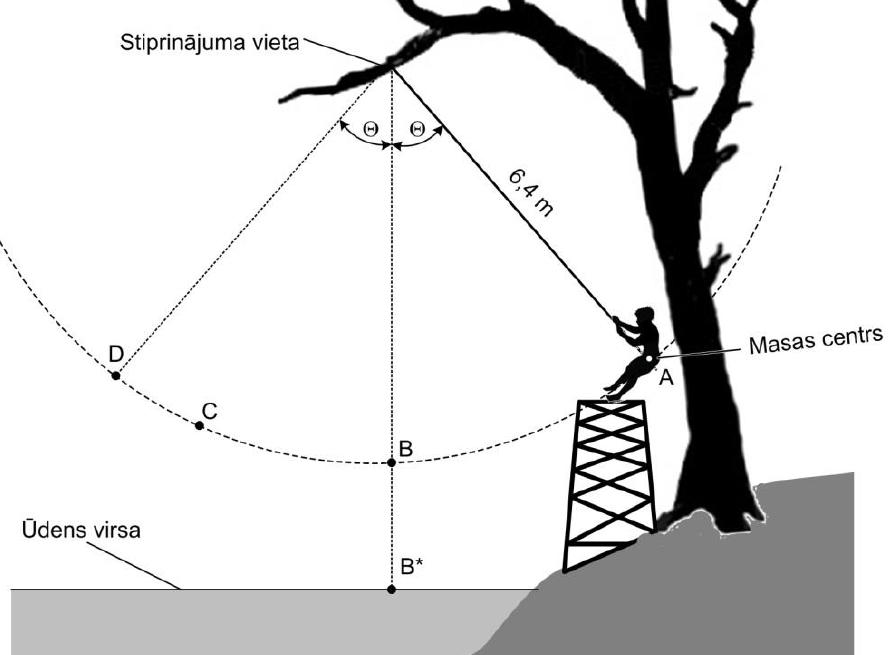
Attālums no virves stiprinājuma punkta līdz zēna masas centram ir \(\mathrm{6,4\space m}\). Punkti A un D atrodas vienādā augstumā \(\mathrm{4,1\space m}\) virs ūdens virsas. Gaisa pretestību, virves masu un deformāciju var neņemt vērā. Pieņemt, ka brīvās krišanas paātrinājuma vērtība ir \(\mathrm{10\space m/s^2}\).
1. Zēns atrodas uz paaugstinājuma punktā A un no miera stāvokļa uzsāk kustību. Zēns atlaiž virvi tad, kad pirmo reizi sasniedz punktu C. Attēlo dotajā zīmējumā zēna masas centra trajektoriju no virves atlaišanas momenta punktā C līdz ūdens virsas sasniegšanai!
2. Otrajā reizē zēns atkārto lēcienu, bet atlaiž virvi tad, kad pirmoreiz sasniedz punktu D. Attēlo dotajā zīmējumā ar citu krāsu zēna masas centra trajektoriju no virves atlaišanas momenta punktā D līdz ūdens virsas sasniegšanai!
3. Zēna masa ir \(\mathrm{50\space kg}\). Aprēķini zēna potenciālo enerģiju attiecībā pret ūdens virsu, kad viņš atrodas punktā A!
4. Punkts B ir svārstību kustības trajektorijas zemākais punkts, un tas atrodas \(\mathrm{2,4\space m}\) augstumā virs ūdens. Aprēķini zēna ātrumu šajā punktā!
5. Trešajā reizē zēns atlaiž vaļā auklu punktā B. Aprēķini, cik tālu horizontālā virzienā aizlido zēns (rēķinot pa ūdens virsmu no punkta B*). Pieņem, ka viņa ātrums auklas atlaišanas brīdī ir \(\mathrm{8,0\space m/s}\). Šī ātruma vērtība nesakrīt ar iepriekšējā solī aprēķināto vērtību.
6. Salīdzini zēna impulsus punktos B un C, neveicot aprēķinus!
1. Zēna masas centra kustības trajektorija ir riņķa līnijas loks \(\mathrm{\cup AD}\). Masas centra lineārais ātrums ir vērsts pa pieskari trajektorijai (skatīt attēlu).
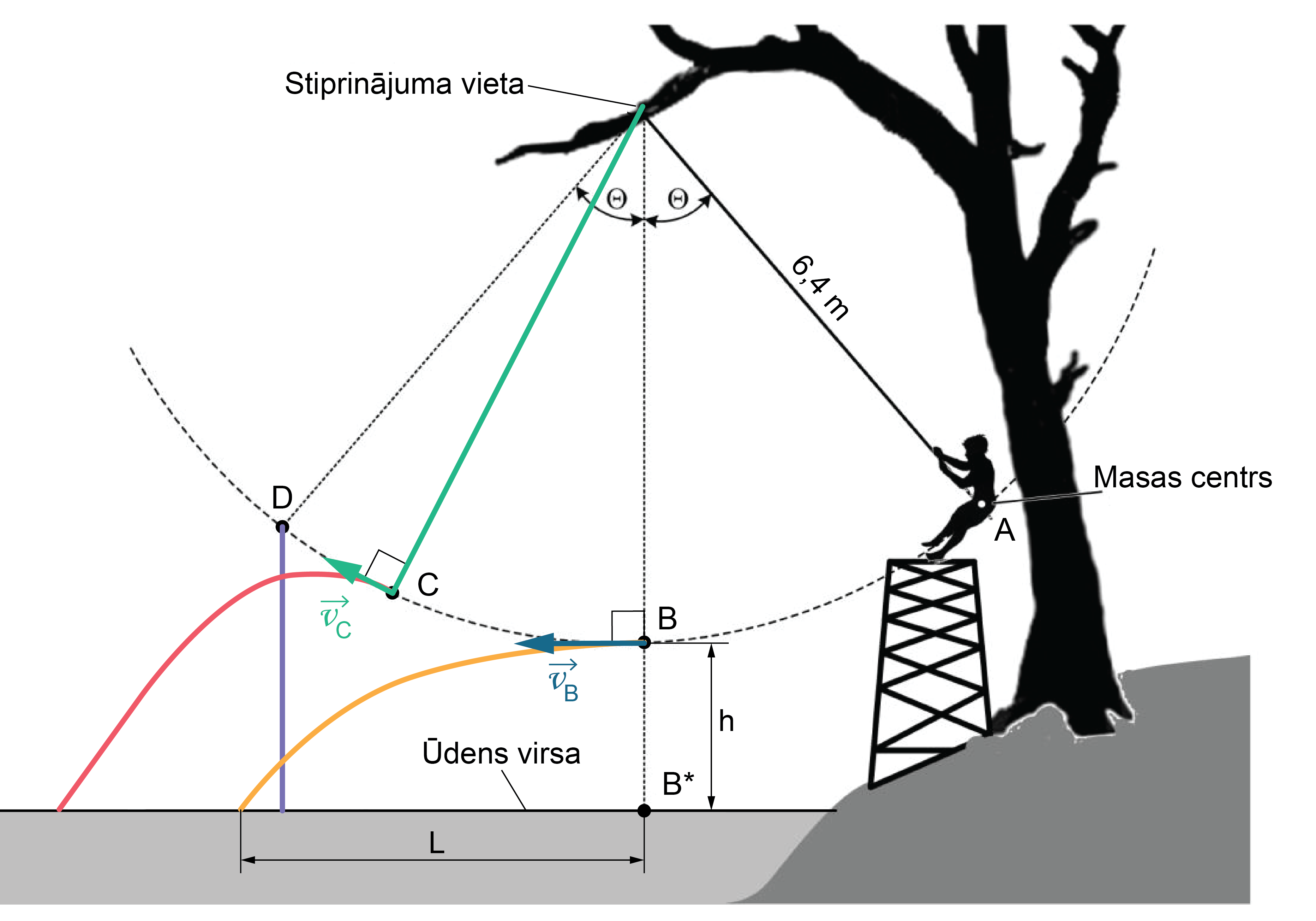
No brīža, kad zēns atlaiž virvi punktā \(\mathrm{C}\), zēna masas centra kustību aplūko, kā slīpi pret horizontu izsviesta ķermeņa kustību. Sākuma ātrums \(\overrightarrow{v_\mathrm{c}}\) punktā \(\mathrm{C}\) ir vērsts leņķī pret horizontu (skatīt attēlu). Zēna kustību nosacīti sadala divos savstarpēji perpendikulāros virzienos. Kustības laikā uz ķermeni darbojas vienīgi smaguma spēks, kas vērsts vertikāli lejup. Sākuma ātrums vērsts slīpi uz augšu, tāpēc zēns vēl kādu brīdi pēc virves atlaišanas inerces dēļ kustas uz augšu, kamēr sasniedz maksimālo augstumu. Pēc maksimālā augstuma sasniegšanas, zēns sāk krist ar brīvās krišanas paātrinājumu. Horizontālā virzienā uz zēnu spēki nedarbojas, tāpēc viņš kustas vienmērīgi ar nemainīgu ātrumu. Rezultātā zēna masas centra trajektorija ir parabolas posms ar zariem, kas vērsti uz leju (attēlā trajektorija ir parādīta ar sarkanu līniju).
2. Zēna masas centra kustību aplūko kā diega svārsta kustības fragmentu. Punktos \(\mathrm{A}\) un \(\mathrm{D}\) masas centra kustības ātrums ir vienāds ar nulli, bet punktā \(\mathrm{B}\) zēna masas centra kustības ātrums \(\overrightarrow{v_\mathrm{B}}\) ir maksimālais (skatīt attēlu). Punktā \(\mathrm{D}\) zēna ātrums ir nulle. Tanī brīdī, atlaižot virvi, zēns uzsāk brīvo kritienu. Viņa masas centra trajektorija ir vertikālā taisne (attēlā trajektorija ir parādīta ar violetu krāsu).
3. Zēna potenciālo enerģiju \(W_\mathrm p\) punktā \(\mathrm A\) attiecībā pret ūdens virsu aprēķina pēc formulas \(W_\mathrm {p}=mgh_\mathrm A\), kur \(m\) – zēna masa, \(g\) – brīvās krišanas paātrinājums, \(h_\mathrm A\)– zēna masas centra augstums virs ūdens virsas.
Aprēķini:
\(W_\mathrm p=mgh_\mathrm A=50\cdot 10\cdot 4,1=2050\space\mathrm J\approx2,1\cdot10^3\space\mathrm J\). Rezultātu noapaļo līdz diviem zīmīgajiem cipariem tādēļ, ka uzdevuma nosacījumos dotajiem skaitļiem ir divi zīmīgie cipari.
Atbilde: zēna potenciālā enerģija punktā \(\mathrm A\) ir \(2,1\cdot10^3\space\mathrm J\).
4. Zēna ātrumu punktā \(\mathrm B\) aprēķina, izmantojot pilnās mehāniskās enerģijas nezūdamības likumu. Pilnā mehāniskā enerģija \(W\) visos kustības trajektorijas punktos ir nemainīga. Pilnā mehāniskā enerģija ir potenciālās \(W_\mathrm p\) un kinētiskās \(W_\mathrm k\) enerģijas summa: \(W=W_\mathrm p +W_\mathrm k=\mathrm{const}\)
Aplūko sākuma punktu \(\mathrm A\) un trajektorijas zemāko punktu \(\mathrm B\). Punktā \(\mathrm A\) pilno mehānisko enerģiju veido tikai potenciālā enerģija \(W_\mathrm {pA}=mgh_\mathrm A\), jo kustība notiek no miera stāvokļa. Punktā \(\mathrm B\) zēnam piemīt gan potenciālā enerģija \(W_\mathrm {pB}=mgh_\mathrm B\), gan kinētiskā enerģija \(W_\mathrm {kB}=\frac{mv^2_\mathrm B}{2}\). Apzīmējumi formulās: \(h_\mathrm B\) – zēna masas centra augstums virs ūdens virsas punktā \(\mathrm B\), \(v_\mathrm B\) – zēna kustības ātrums punktā \(\mathrm B\).
Uzraksta mehāniskās enerģijas nezūdamības likumu: \(mgh_\mathrm A=mgh_\mathrm B+\frac{mv^2_\mathrm B}{2}\). No vienādojuma izsaka zēna kustības ātrumu \(v_\mathrm B\) punktā \(\mathrm B\): \(v_\mathrm B=\sqrt{2g(h_\mathrm A-h_\mathrm B)}\).
Aprēķini: \(v_\mathrm B=\sqrt{2g(h_\mathrm A-h_\mathrm B)}=\sqrt{2\cdot 10\cdot(4,1-2,4)}\approx 5,8\space\mathrm {m/s}\).
Risināt var arī pa soļiem. Aprēķina zēna potenciālo enerģiju punktos \(\mathrm A\) un \(\mathrm B\) un kinētisko enerģiju punktā \(\mathrm B\), kā starpību starp potenciālajām enerģijām punktos \(\mathrm A\) un \(\mathrm B\). No kinētiskās enerģijas formulas izsaka zēna ātrumu \(v_\mathrm B\) punktā \(\mathrm B\) un veic aprēķinus.
Aprēķini:
\(W_\mathrm {pA}=mgh_\mathrm A=50\cdot10\cdot4,1=2050\space\mathrm J\approx2,1\cdot10^3\space\mathrm J\).
\(W_\mathrm {pB}=mgh_\mathrm B=50\cdot10\cdot2,4=1200\space\mathrm J=1,2\cdot10^3\space\mathrm J\).
\(W_\mathrm {kB}=W_\mathrm {pA}-W_\mathrm {pB}=2,05\cdot10^3-1,20\cdot10^3=0,85\cdot10^3\space\mathrm J\).
No formulas \(W_\mathrm {kB}=\frac{mv^2_\mathrm B}{2}\) izsaka \(v_\mathrm B=\sqrt{\frac{2W_\mathrm{kB}}{m}}\) un ievieto skaitliskās vērtības \(v_\mathrm B=\sqrt{\frac{2\cdot0,85\cdot10^3}{50}}\approx5,8\space\mathrm{m/s}\).
Atbilde: zēna ātrums punktā \(\mathrm B\) ir aptuveni \(5,8\space \mathrm{m/s}\).
5. Pēc virves atlaišanas punktā \(\mathrm B\) zēna sākuma ātrums ir vērsts horizontāli (skatīt attēlu). Tādēļ pa vertikāli notiek brīvā krišana, pa horizontāli – vienmērīga kustība ar nemainīgu ātrumu.
Lidojuma tālumu horizontālā virzienā \(L\) (skatīt attēlu) nosaka pēc formulas \(L=v_\mathrm Bt\), kur \(v_\mathrm B\) – kustības ātrums punktā \(\mathrm B\), \(t\) – kustības laiks.
Lidojuma laiku aprēķina no vertikālās kustības sakarībām. Brīvā krišana ir vienmērīgi paātrināta kustība ar brīvās krišanas paātrinājumu \(g\) no miera stāvokļa. Pārvietojuma moduli dotajā gadījumā apzīmē ar \(h\): \(h=\frac{gt^2}{2}\). Izsaka kustības laiku vai lidojuma ilgumu \(t=\sqrt{\frac{2h}g{}}\).
Formulā \(L=v_\mathrm Bt\) ievietojot izteiksmi \(t=\sqrt{\frac{2h}g{}}\), iegūst lidojuma tāluma aprēķina formulu: \(L=v_\mathrm B\sqrt{\frac{2h}{g}}\).
Aprēķini: \(L=v_\mathrm B\sqrt{\frac{2h}{g}}=8,0\cdot\sqrt{\frac{2\cdot2,4}{10}}\approx5,5\space\mathrm m\)
Var risināt pa soļiem: \(t=\sqrt{\frac{2h}g{}}=\sqrt{\frac{2\cdot2,4}{10}}\approx0,69\space\mathrm s\) \(L=v_\mathrm B t=8\cdot0,69\approx5,5\space\mathrm m\)
Atbilde: horizontālajā virzienā zēns aizlido aptuveni \(5,5\space\mathrm m\) attālumā.
6. Ķermeņa impulsa \(p\) aprēķina formula ir \(p=mv\), kur \(m\) – ķermeņa masa, \(v\) – ķermeņa kustības ātrums. No formulas redzams, ka vienam un tam pašam ķermenim lielāks impulss ir tad, ja tas kustas ātrāk. Zēna ātrums punktā \(\mathrm B\) ir lielāks nekā punktā \(\mathrm C\), tādēļ zēna impulss punktā \(\mathrm B\) ir lielāks nekā punktā \(\mathrm C\).
1. skaidrojums: ja zēna kustību aplūko kā diega svārsta svārstības, tad punktā \(\mathrm B\) zēns šķērso līdzsvara stāvokli – kustības ātrums ir maksimālais. Palielinoties novirzei no līdzsvara stāvokļa, uzdevumā – punktā \(\mathrm C\), ātrums samazinās.
2. skaidrojums: izmanto pilnās mehāniskās enerģijas nezūdamības likumu. Punktā \(\mathrm B\) zēnam piemīt vismazākā potenciālā enerģija un vislielākā kinētiskā enerģija. Kustoties punkta \(\mathrm C\) virzienā, zēna potenciālā enerģija palielinās, bet kinētiskā enerģija samazinās. Ja samazinās kinētiskā enerģija, tad samazinās zēna kustības ātrums un impulss.
Vērtēšanas kritēriji
1. Zīmē trajektorijas līkni no punkta C – 1 punkts.
2. Zīmē trajektorijas līkni no punkta D – 1 punkts.
3. Zina vai atrod formulu lapā potenciālās enerģijas aprēķināšanas formulu un aprēķina enerģiju – 1 punkts.
4. Izmanto enerģijas nezūdamības likumu – 1 punkts.
Aprēķina ātrumu punktā B – 1 punkts.
5. Zina vienmērīgi paātrinātas kustības ceļa formulu un aprēķina krišanas laiku – 1 punkts.
Zina vienmērīgas kustības ceļa formulu un aprēķina lidojuma tālumu – 1 punkts.
6. Skaidro, kurā kustības punktā – B vai C – zēna impulss ir lielāks – 1 punkts.