Praksē dažādi produkti tiek pārvietoti, izmantojot cauruļvadus. Piemēram, cauruļvados var tikt pārvietota nafta, gāze vai ūdens. (1. att. a) Arī mājas bez cauruļvadu transporta ir grūti iztikt, jo sadzīvē ir nepieciešama gan dzeramais ūdens, gan gāze (1. att. b), gan arī siltumu ziemā nodrošina siltais ūdens, kas tiek pievadīts radiatoriem.

1. att. Cauruļvadu izmantošana
Gan cauruli, gan tajā plūstošo šķidrumu vai gāzi var raksturot ar dažādiem fizikālajiem lielumiem, kuri ir savstarpēji saistīti (2. att.). Šķidrumu raksturo šādi lielumi:
v - kustības ātrums, m/s
ρšķ - šķidruma blīvums, kg/m3
Cauruli raksturo fizikālais lielums:
S - šķērsgriezuma laukums, m2
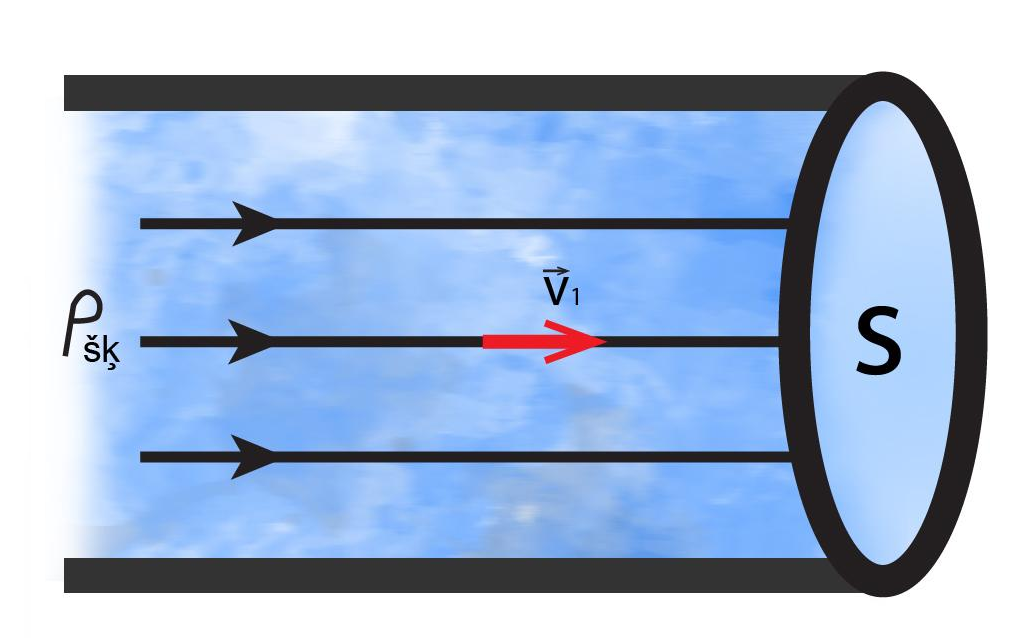
2. att. Cauruli un plūstošo šķidrumu raksturojošie fizikālie lielumi
Šie fizikālie lielumi ir savstarpēji saistīti. Ja, piemēram, ūdens caurule ir ar mainīgu šķērsgriezuma laukumu (3. att.), tad caur katru šķērsgriezumu vienādos laika momentos izplūst viens un tas pats ūdens tilpums. No tā seko, ka caurules posmu šķērsgriezumu attiecība ir vienāda ar apgriezto ātrumu attiecību caurules posmos jeb S1/S2=v2/v1.
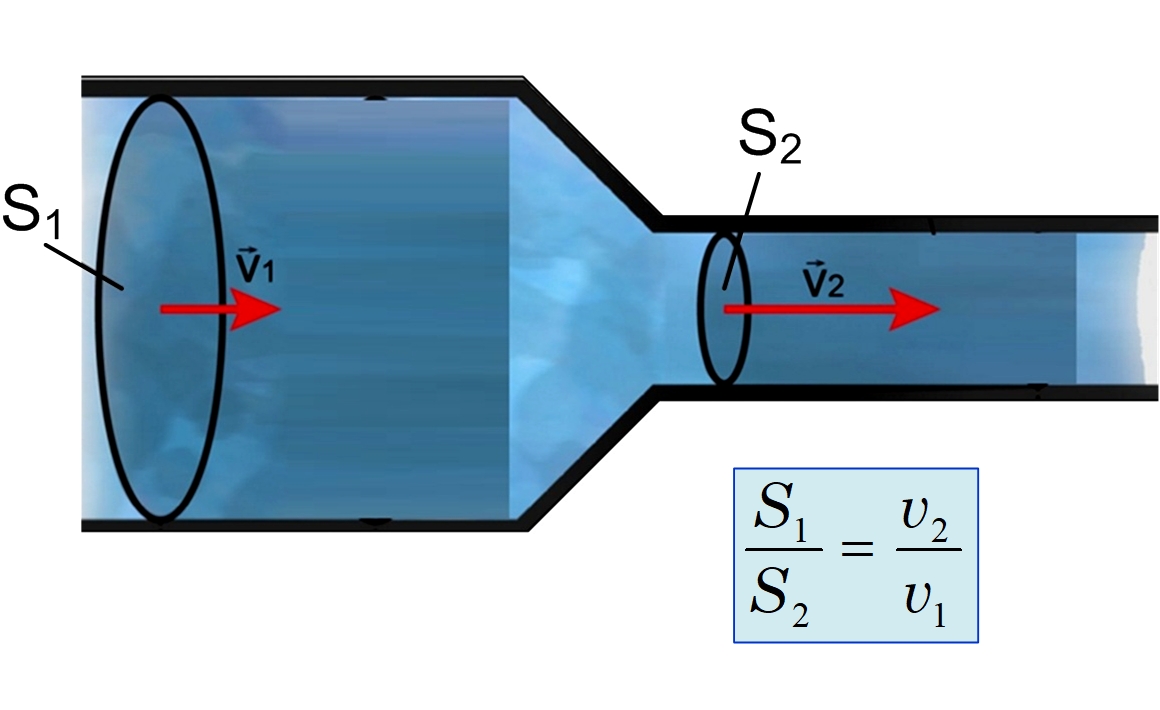
3. att. Caurules šķērsgriezuma ietekme uz plūsmas ātrumu
Plūsmas raksturošanai ir svarīgi vēl citi fizikāli lielumi. Plūsmai ir spiediens p, kas rodas kustības dēļ, un to sauc par dinamisko spiedienu. Dinamiskais nav tas pats statiskais spiediens, kas ir, piemēram, atmosfēras spiediens vai cilvēka spiediens uz zemi. Ja salīdzina dinamisko spiedienu dažādiem plūsmas ātrumiem, tad vietās, kur plūsma ir lēnākā spiediens ir lielāks un otrādi, kur plūsmas ātrums palielinās, dinamiskais spiediens samazinās(4. att.)
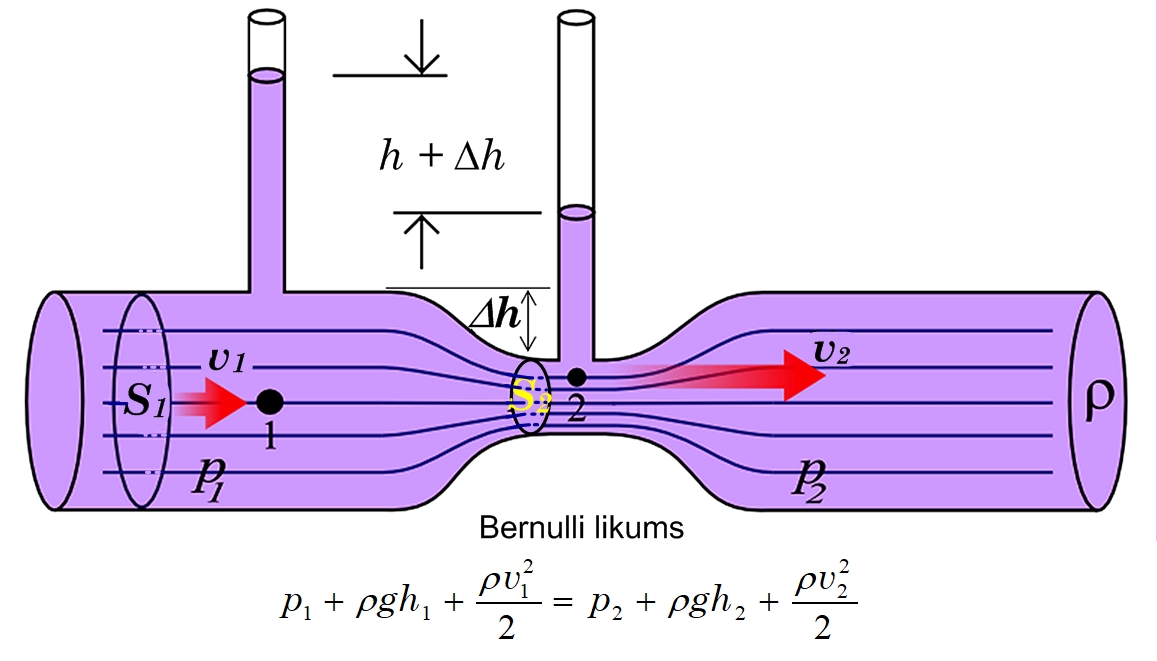
4. att. Dinamiskā spiediena izmaiņas atkarībā no plūsmas ātruma
Lai iegūtu sakarību, kas saista caurules šķersgriezuma laukuma S un plūsmas ātruma v, jāņem vērā tas, ka caur jebkuru šķērsgriezumu laukumu vienādos laika momentos izplūst viens un tas pats ūdens tilpums (1. att.). Ja šķersgriezuma laukumi ir S1 un S2 plūsmas ātrumi attiecīgi v1 un v2, bet apskatītais laika moments ∆t, tad no tilpumu vienādības seko, ka v1S1∆t=v2S2∆t jeb v1S1=v2S2. Tas nozīmē, ka šķidruma vai gāzes plūsmas ātrums caurulē ir apgriezti proprocionāls plūsmas šķērsgriezuma laukumam un v1/v2=S2/S1.
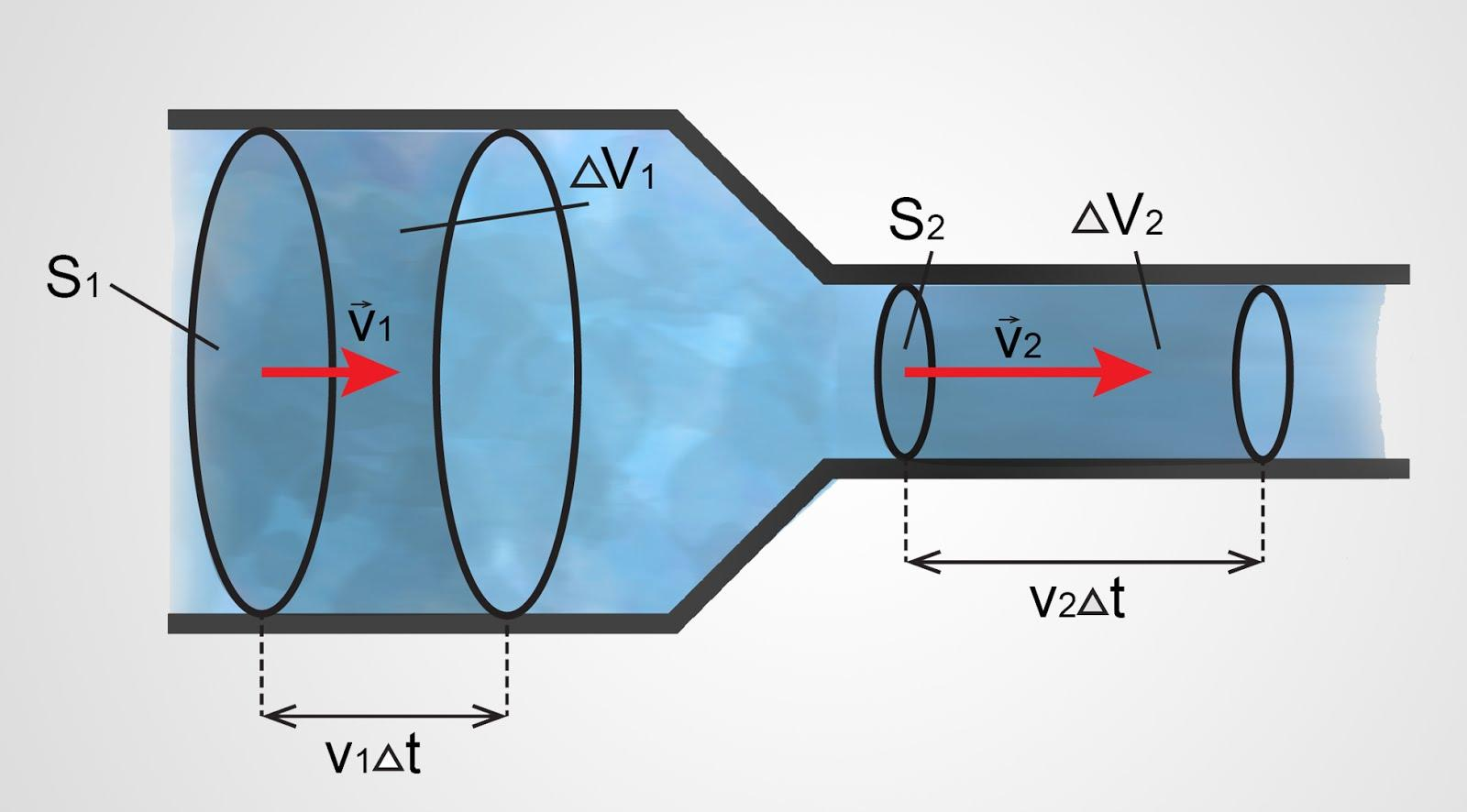
1. att. Caurules šķērsgriezuma ietekme uz plūsmas ātrumu
Plūsmas ātruma izmaiņa ietekmē plūsmas dinamisko spiedienu. Šis fakts ir ļoti nozīmīgs dažādos tehnoloģiskos risinājumos un ikdienišķās parādībās. Piemēram, cēlējspēka gadījumā, kas nodrošina lidmašīnām spēju lidot (2. att.). Spārna šķērsgriezumā var redzēt, ka virspuse ir vairāk izliekta nekā apakšpuse, tas nodrošina virs spārna lielāku plūsmas ātrumu un mazāku dinamisko spiedienu. Arī dzīvajā dabā ir piemēri, kad dzīvnieks panāk cēlējspēka ietekmi, piemērma, ir tāda “lidojošā” čūska, kas izplešs savas ribas un iegūst ķermeņa formu, kas palielina saskares laukumu un atbilst nosacījumiem, lai parādītos cēlējspēks. Noskaties video!

2. att. Cēlējspēka rašanās
Sacīšu automašīnām praksē lieto antispārnu, kas darbojas līdzīgi lidmašīnas spārnam, tikai pretējā virzienā. Tas ir nepieciešams tādēļ, ka braucot ar lielu ātrumu, mašīnai ir nepieciešama labāka saķere ar ceļu, lai nezaudētu kontroli. Anti spārns (3. att.) ir novietots tā, ka gaisa plūsma zem tā ir ātrāka, līdz ar to uz antispārnu un līdz ar to arī uz mašīnu, darbojas lejup vērst spēks, kas palielina mašīnas saķeri ar zemi.
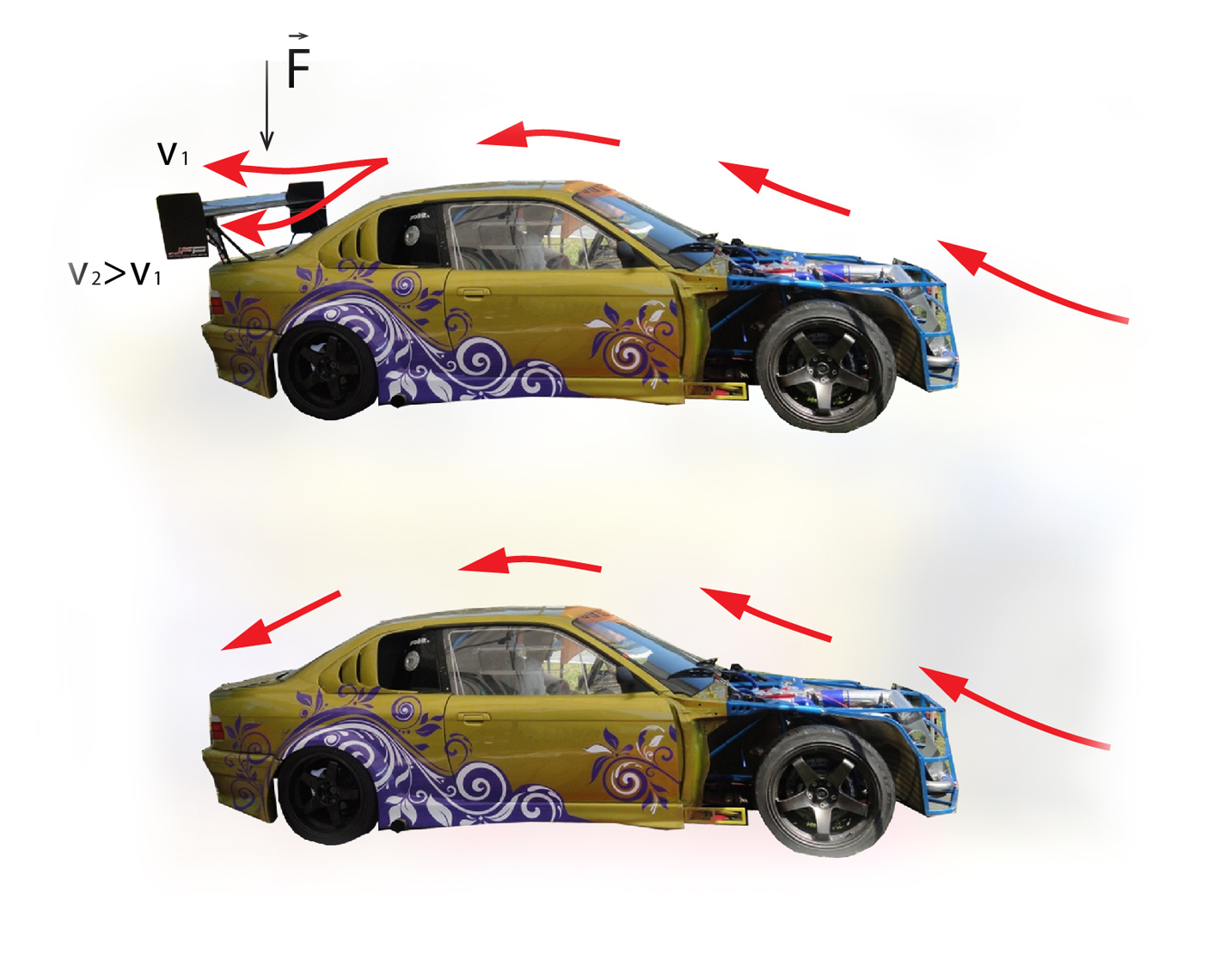
3. att. Automašīnas anti spārns
Šķidrumos un gāzēs novērojams Magnusa efekts, kas rodas tad, ja šķidrumā vai gāzē pārvietojas rotējošs objekts, piemēram, iegrieztas bumbas kustība gaisā. Rotējošā bumba berzes dēļ velk līdzi sev gaisu, tādēļ plūsmas ātrums vienā virzienā ir lielāks nekā otrā. Šī spiedienu starpība atkal izraisa uz objektu darbojošu spēku (4. att. a). Magnusa efektu izmantot dažādos sporta veidos, piemēram, galda tenisā un futbolā. Iegriežot bumbu, tai tiek radīta ieliekta kustības trajektorija, kas pretiniekam izraisa papildus grūtības (4. att. b).

4. att. Magnusa efekts
Ja uz cilvēku pēdu paskatās profilā, tad izstieptā stāvoklī tā ļoti atgādina lidmašīnas spārnu. Līdz ar to, ja peld ar izstieptu pēdu, tad uz kāju darbojas cēlējspēks, līdzīgi kā lidmašīnai, un peldēt ir vieglāk (5. att.).
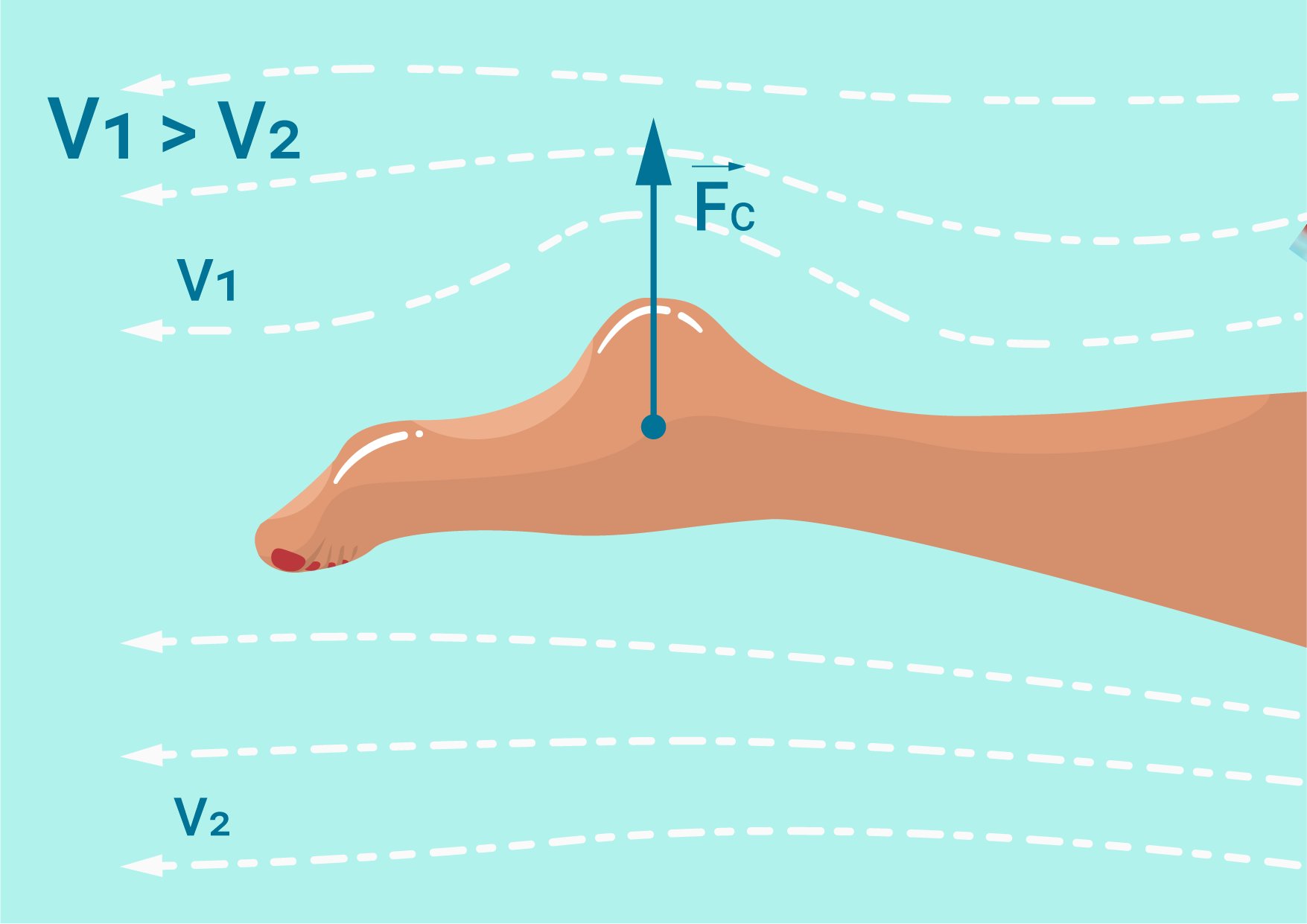
5. att. Šķidruma plūsmas ietekme uz peldēšanu
Šķidruma un gāzu plūsmas izpausmes var būt arī ar negatīvām sekām. Ja vēja plūsma kustas pāri jumtam (6. att.), tad tālākā jumta puse tiecas pacelties gaisā, jo gaisa plūsma pazemina spiedienu virs jumta, līdz ar atmosfēras spiediens, kas darbojas uz jumta apakšu, ir lielāks nekā spiediens virs jumta, un jumts tiek pakļaut spēka ietekmei no apakšas, kas rodas spiedienu starpības dēļ. Šādu parādību var dažkārt novērtot vētras laikā.

6. att. Gaisa plūsma var noraut jumtu
Vēl viens fizikālais lielums, kas ir svarīgs šķidruma plūsmas gadījumā, ir plūsmas augstums virs zemes h, jo tas izmaina potenciālo enerģiju. 18. gs. Šveiciešu matemātiķis un fiziķis Dāniels Bernulli apvienoja šo un iepriekšminētos fizikālos lielumus vienā vienādojumā, kas mūsdienās pazīstams kā Bernulli likums (1. att.). Balstoties uz Bernulli likumu p+ρv2/2+ρgh=const, kur
p - dinamiskais spiediens, Pa
ρ - šķidruma vai gāzes blīvums, kg/m3
v - plūsmas ātrums, m/s
g - brīvās krišanas paātrinājums, m/s2
h - plūsmas augstums, m
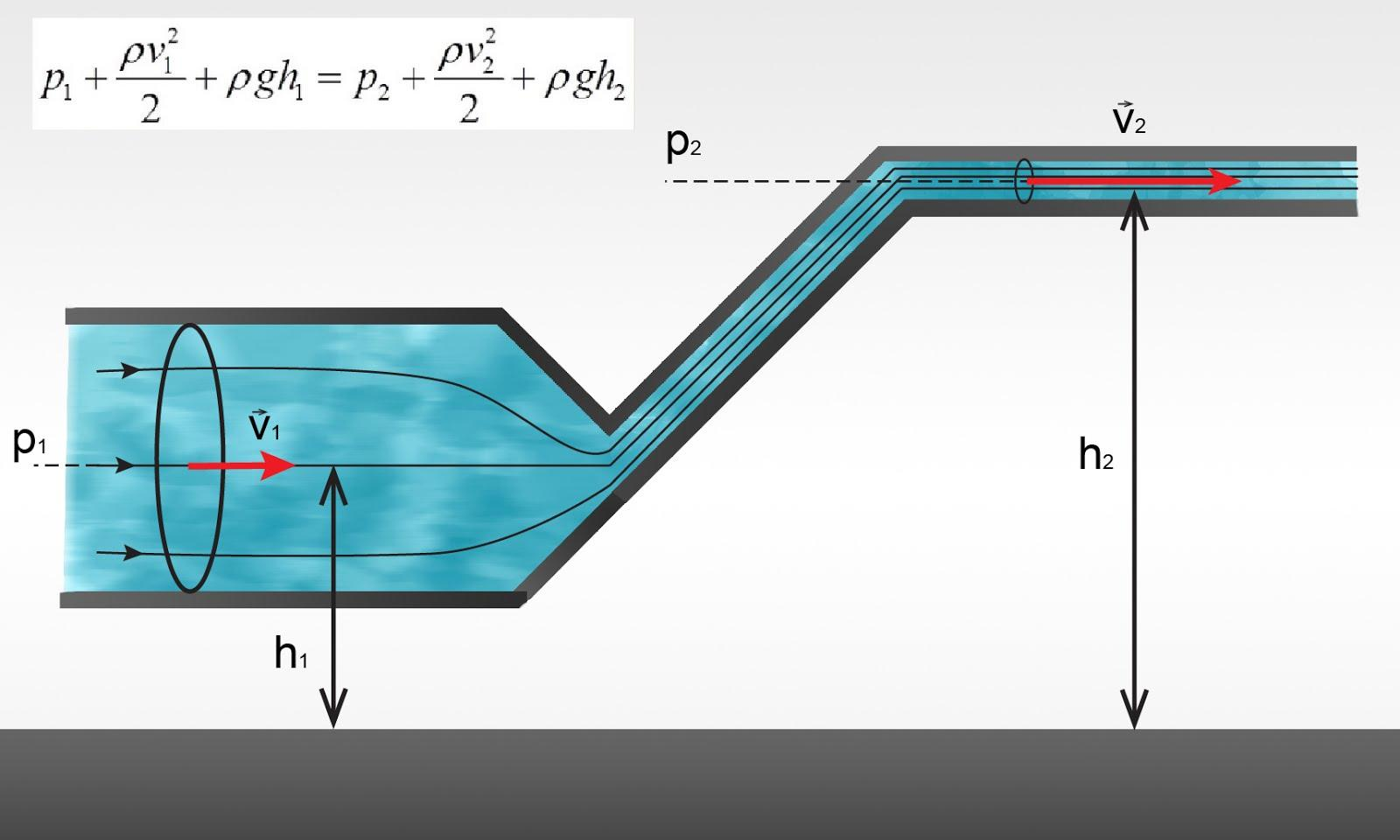
1. att. Berulli likums
Ir dažādi veidi kā var pētīt šķidruma un gāzes plūsmas ap dažādiem ķermeņiem. Var lietot vēja tuneļus, kuros tiek radītās vizuāli saskatāmas gāzes plūsmas (2. att.). Līdz ar to iespējams saskatīt kur plūsma ir vienmērīga, bet kurās vietās rodas plūsmas virpuļi.

2. att. Spārna profils paštaisītā vēja tunelī
Izmantojot zināmos fizikas likumus, plūsmu uzvedību iespējams arī modelēt. Fizikas un matemātikas fakultātē ir studiju kursi, kuros apgūst dažāda veida plūsmas modelēšanu ap dažāda veida objektiem. Plūsmas uzvedība ir atkarīga gan no dažādiem plūsmas, gan arī objekta fizikālajām īpašībām (3. att.).
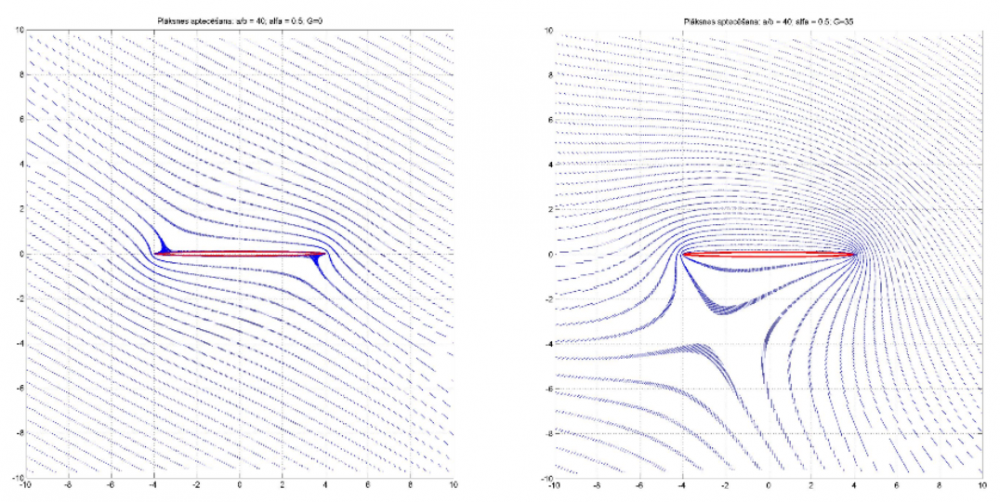
3. att. Plūsmas modelēšana