Paveroties naksnīgajās debesīs, varam redzēt simtiem zvaigžņu un zvaigznājus, spožo Mēnesi, un ja paveicās, tad arī kādu citu planētu. Šad un tad ieraugāma ir mākslīgie pavadoņi, kas nu jau čum un mudž dažādās orbītās ap Zemi. Lai gan ar aci pirmajā brīdī tas nav ieraugāms, tomēr pavērojot ilgāk vai fotografējot debesis ar lielu ekspozīcijas laiku (1. att. a) var redzēt, ka zvaigznes pie debess juma kustas, turklāt pa riņķveida trajektorijām. Zemes rotācijas dēļ zvaigznes pie debesīm atrodas šķietamā rotācijas kustībā ap Polārzvaigzni. Šī iemesla dēļ dažādos gadalaikos un dažādās nakts stundās atšķirās zvaigznāji un zvaigznes, ko varam saskatīt. Zvaigžņu redzamības paredzēšanai vai zvaigznāju un zvaigžņu atpazīšanai var lietot zvaigžņu karti, kas attēlo zvaigžņu redzamo stāvokli mūsu izvēletajā laikā (1. att. b). Mūsdienās pieejamas arī lietotnes mobilajiem telefoniem, kas lietojamas zvaigžņu karšu vietā.

1. att. Zvaigžņotās debess kustība un zvaigžņu karte
Ja zvaigžņu kustība ir šķietama, tad planētu kustība Saules sistēmā gan ne. Planētu kustas ap Sauli, jo uz tām darbojas Saules gravitācijas spēks. Planētas tuvināti kustas pa elipses formas orbītām, tomēr tā nav vienīgā likumsakarība, kas raksturo planētu kustību ap Sauli. Matemātiķis Johaness Keplers aprakstīja kopumā trīs likumsakarības, kas tagad pazīstamas kā Keplera likumi.
Pirmais Keplera likums nosaka, ka planētas kustas ap Sauli pa elipsēm, kuras vienā fokusā atrodas Saule (2. att.). Orbītas punktu, kad planēta atrodas vistālāk no Saules, sauc par afēliju, bet tuvāko orbītas punktu Saulei par perihēliju.
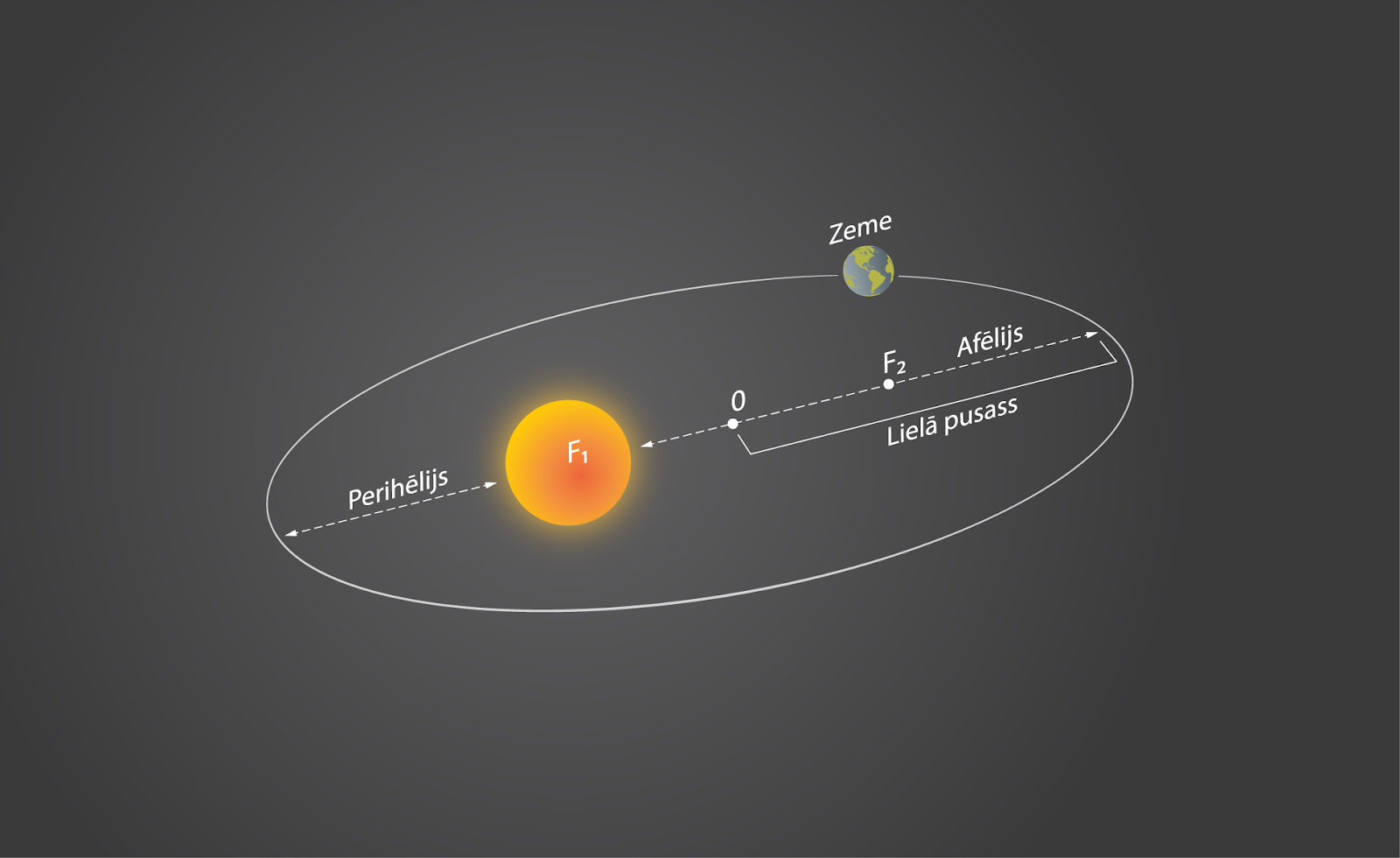
2. att. Pirmā Keplera likuma attēlojums
Otrais Keplera likums nosaka, ka planētas kustas ap Sauli tā, ka nogriežņi, kas savieno planētas centru ar Sauli, vienādos laika intervālos noklāj vienādus laukumus orbītas plaknē. Piemērm, 3. attēlā ar t1, t2, t3 un t4 ir atzīmēti laika momenti, kuros planēta atrodas attiecīgajā orbītas vietā. Ja t2-t1 ir vienāds ar t4-t3 jeb tiek apskatīta planētas kustība vienādos laika intervālos, tad laukumi S1 un S2 ir vienādi. Līdz ar to, ja planētas orbītai ir elipses forma, tad planēta katrā tās punktā nepārvietojas ar vienu un to pašu ātrumu. Tālāk no Saules ātrums ir mazāks, bet tuvojoties Saulei tas palielinās.
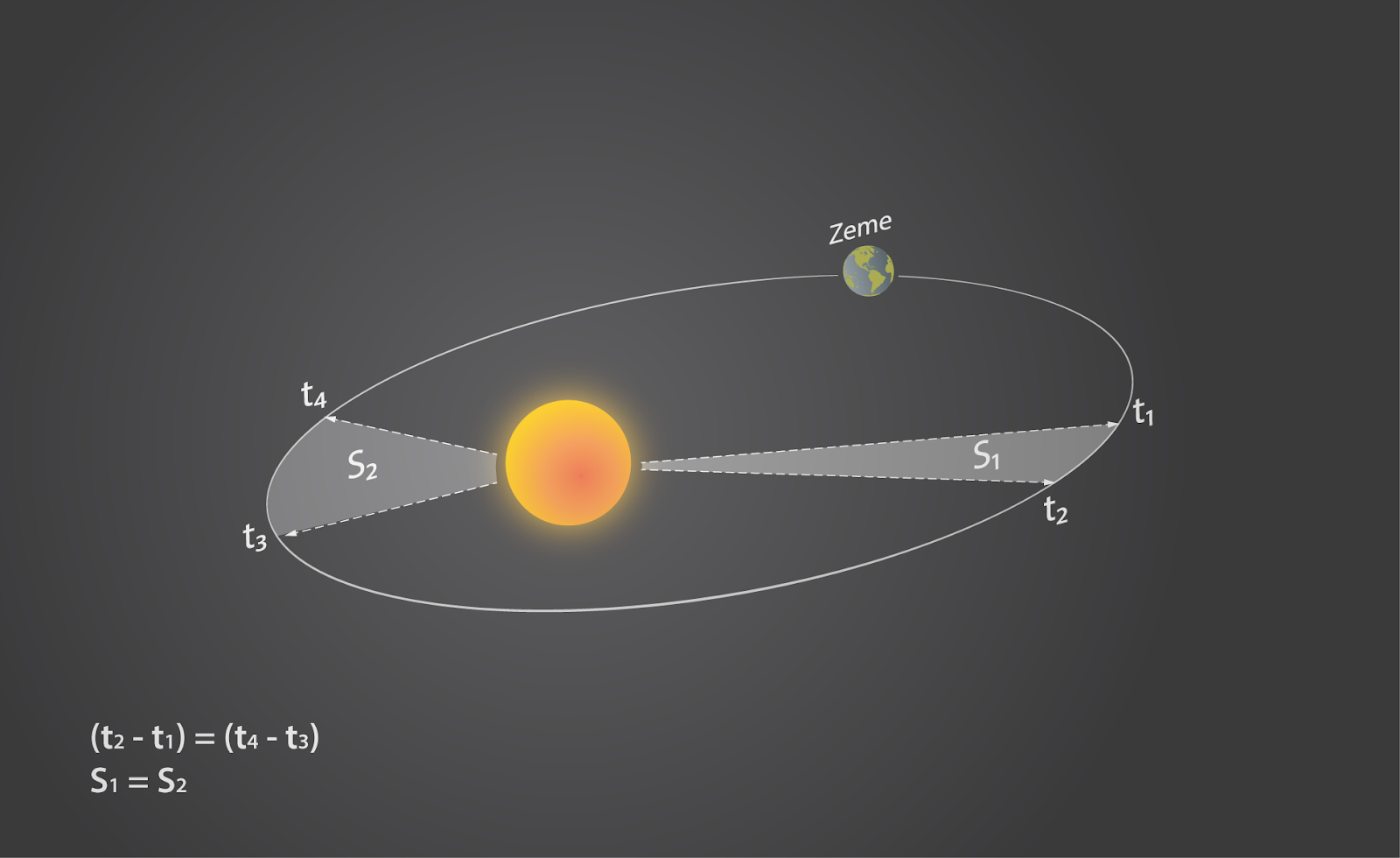
3. att. Otrā Keplera likuma grafiskais attēlojums
Otrai Keplera likums ļoti uzskatāmi parādās komētu kustībā. Viena no pazīstamākajām komētām ir Haleja komēta, kas Zemes tuvumā parādās ik pēc 75 - 76 gadiem un salīdzinoši diezgan ātri pazūd. Tas izskaidrojams ar to, ka komētas orbīta ap Sauli ir ļoti izstiepta (4. att.) un, atrodoties Zemes tuvumā, komēta atrodas arī Saules tuvumā, līdz ar to komētas ātrums ir viens no lielākajiem.
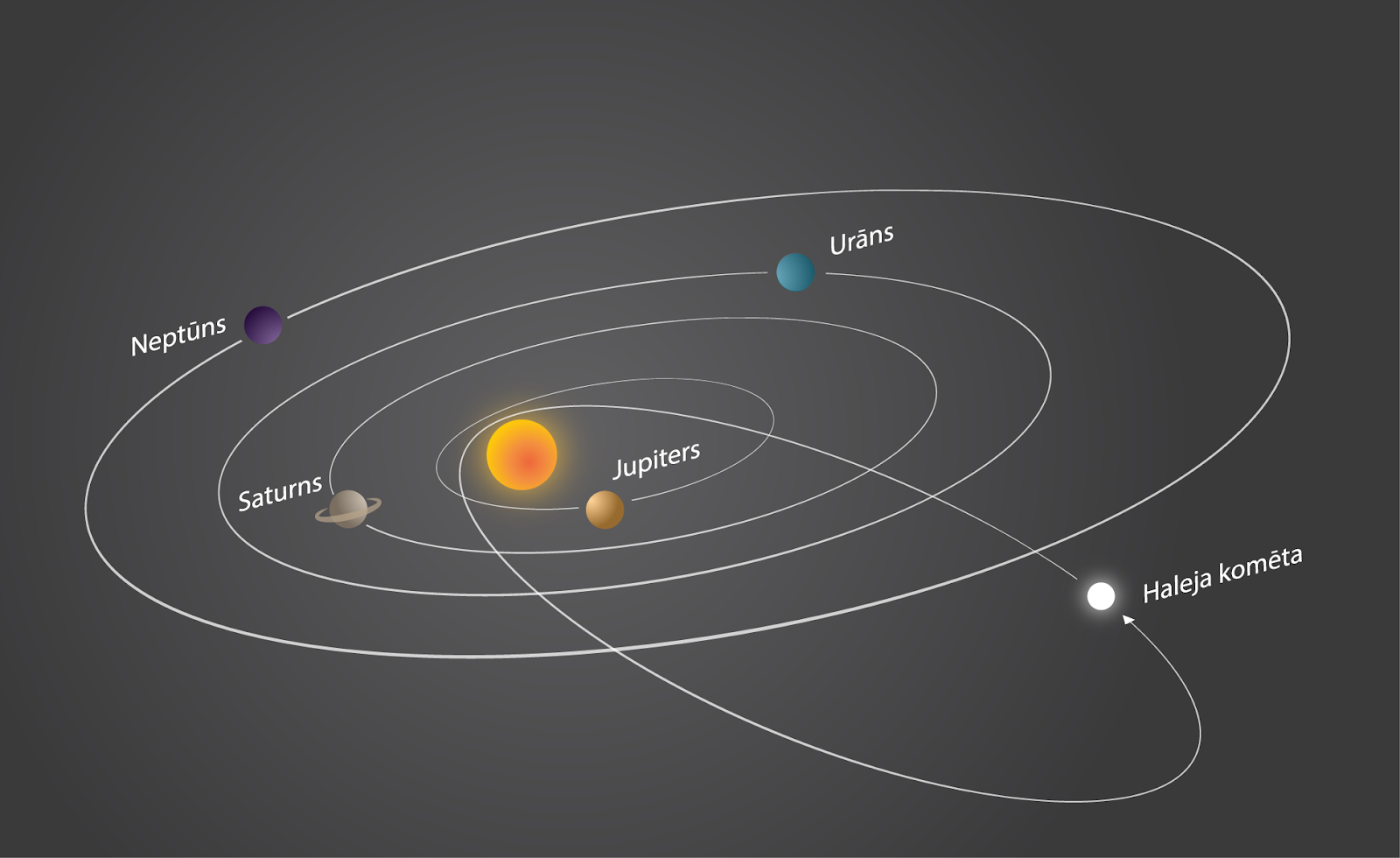
4. att. Haleja komētas orbīta salīdzinājumā ar dažādu Saules sistēmas planētu orbītām
Trešais Keplera likums apraksta to, ka divu planētu apriņķošanas periodu kvadrāti attiecas tāpat kā šo planētu orbītu lielo pusasu kubi. Par orbītas lielo pusasi sauc pusi no nogriežņa, kas savieno perihēlija un afēlija punktus uz planētas orbītas (2. att.). Ja orbītas ir riņkveida, tad lielā pusass vienāda ar orbītas rādiusu (5. att.).
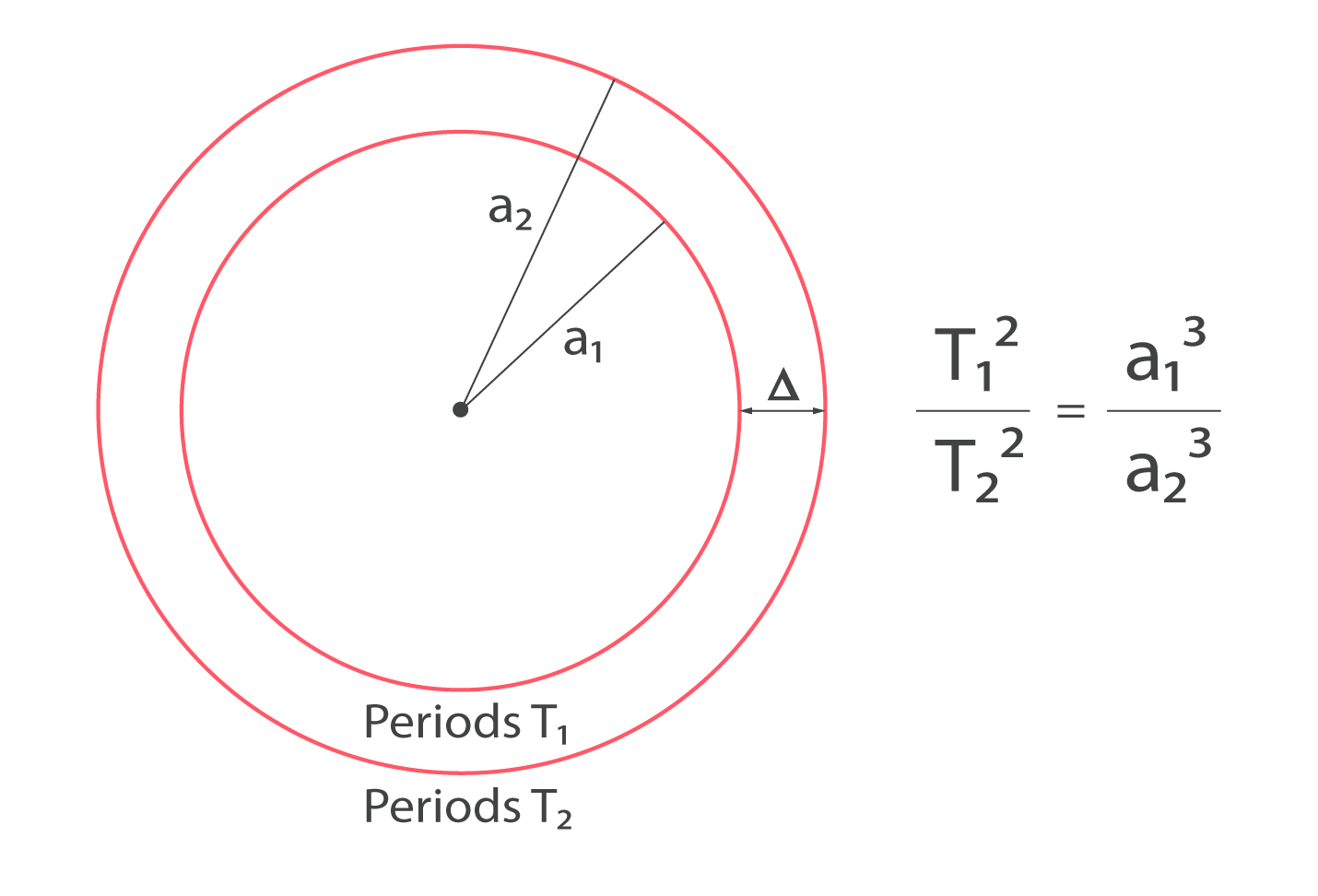
5. att. Trešais Kelpera likums
Ķermeņi, Zemes gravitācijas spēka ietekmē, kustas ne tika Zemes virsmas tuvumā, bet arī lielākā attālumā no tās. Tāds ir Zemes vienīgais dabīgais pavadonis Mēness, kā arī ļoti daudz un dažādu veidu mākslīgie pavadoņi. Kad pavadonis kustas ap Zemi, to orbītā notur Zemes gravitācijas spēks. Tomēr, lai pavadonis nonāktu riņķveida orbītā ap Zemi, tam ir jāpiešķir noteikts ātrums, ko sauc par pirmo kosmisko ātrumu, kura lielums v=7.9 km/s. Ja pavadonim piešķir ātrumu, ka mazāks par pirmo kosmisko ātrumu, tad pavadonis nokrīt uz Zemes (1. att. 1. un 2. trajektorija). Ja pavadonim piešķir pirmo kosmisko ātrumu, tad tas ieiet riņķveida orbītā ap Zemi (1. att. 3. trajektorija), savukārt, ja piešķirtais ātrums ir robežās starp pirmo un otro kosmisko ātrumu, tad pavadoņa orbīta ieņems elipses formu. (1. att. 4. trajektorija). Pārsniedzot otro kosmisko ātrumu, pavadonis izraujas no Zemes gravitācijas un vairs neriņķ ap to (1. att. 5. un 6. trajektorija).
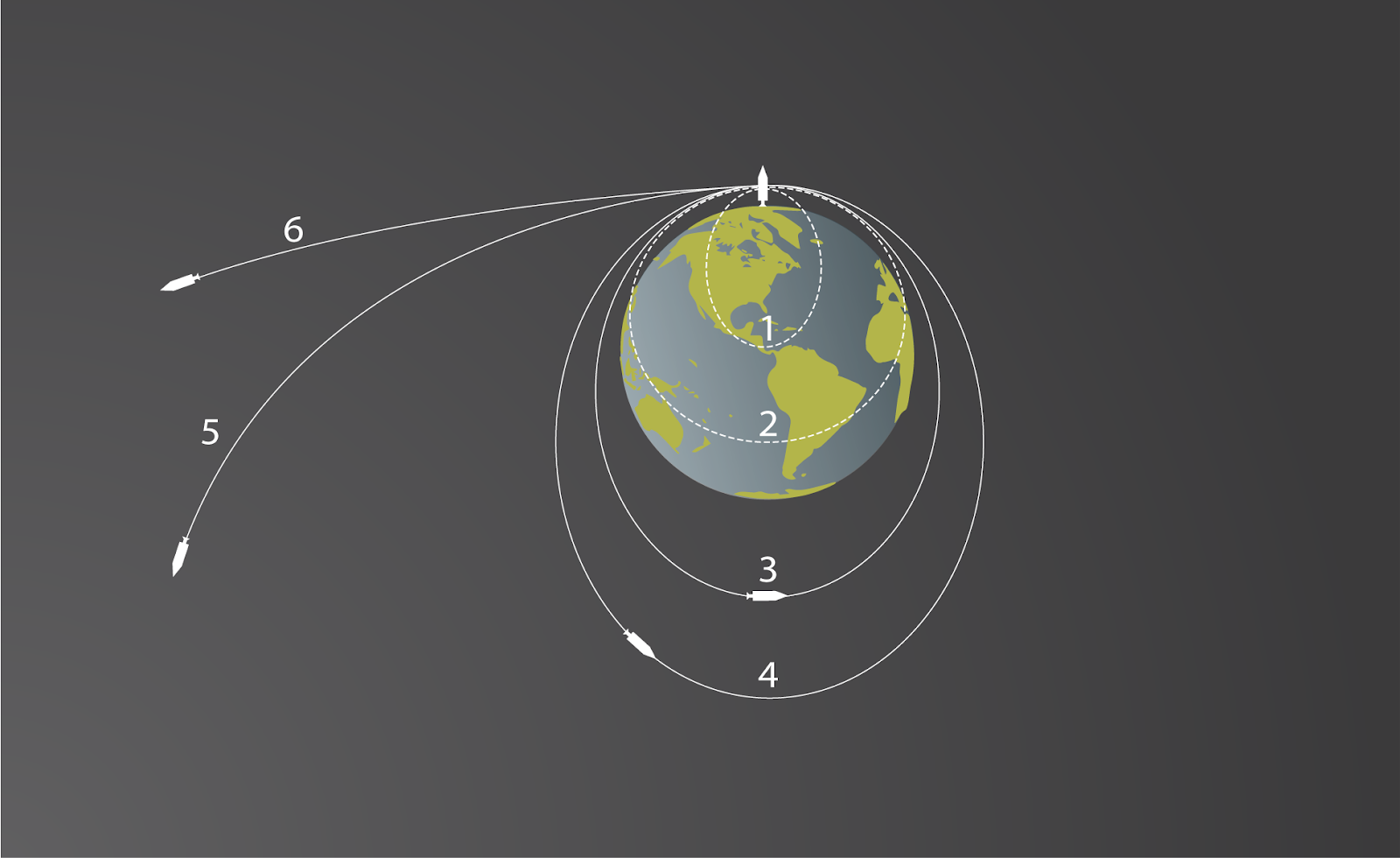
1. att. Dažādas ķermeņu trajektorijas kustībā ap Zemi
Ja pavadonis atrodas riņķveida orbītā ap Zemi (1. att. 3. trajektorija), tad tā kustību raksturo nemainīgs centrtieces paātrinājums, ko nodrošina Zemes gravitācijas spēks (2. att.).
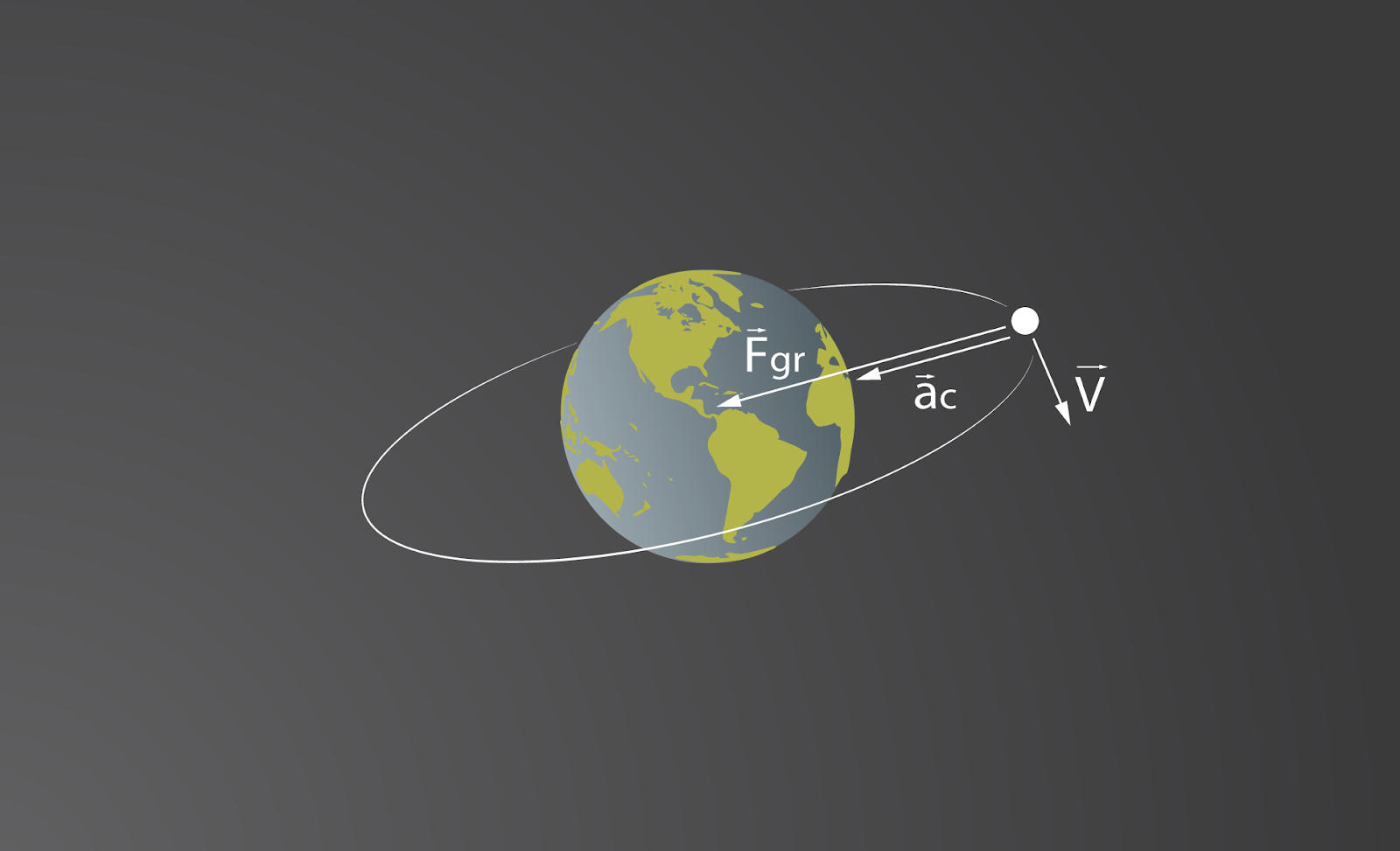
2. att. Centrtieces paātrinājums, kas darbojas uz pavadoni
Ja pirmais kosmiskais ātrums tiek pārsniegts, tad pavadoņa orbītas forma kļūst par elipsi (1. att. 4. trajektorija). Elipse no riņķa līnijas (3. att. a) atšķiras ar to, ka tai ir divi “centri” jeb fokusi (3.att. b) Ja riņķa līnijai ir nemainīgs katra punkta attālums līdz riņķa līnijas centram, tad elipsei saglabājas katra punkta attālumu summa līdz abiem fokusiem, proti, ja paņem jebkurus divus punktus uz elipses un salīdzina nogriežņu garumu summu, kas savieno katru puktu ar abiem fokusiem, tad šīs summas ir vienādas (3. att. b).
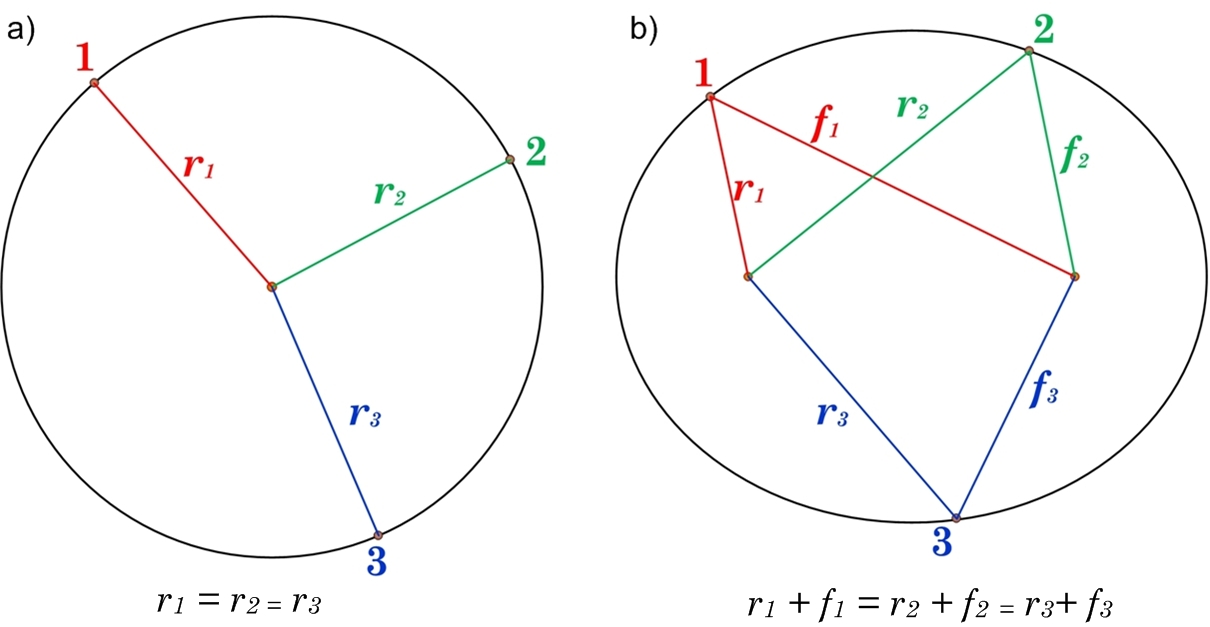
3. att. Riņķa līnijas un elipses salīdzinājums
Jo vairāk pavadonis pārsniedz pirmo kosmisko ātrumu, jo trajektorija ap Zemi kļūst izstieptāka. To var izmantot priekš militārajiem pavadoņiem, jo šādās orbītās pavadoņi var ļoti pietuvoties Zemes virsmai, kas paver iespējas novērot, kas notiek kādas valsts teritorijā. Ja pavadonis sasniedz ātrumu 11.2 km/s, tad tas pārvar Zemes pievilkšanās spēku (1. att. 5. un 6. trajektorija) un iekļūst orbītā ap Sauli. Šo ātrumu sauc par otro kosmisko ātrumu (4. att.).
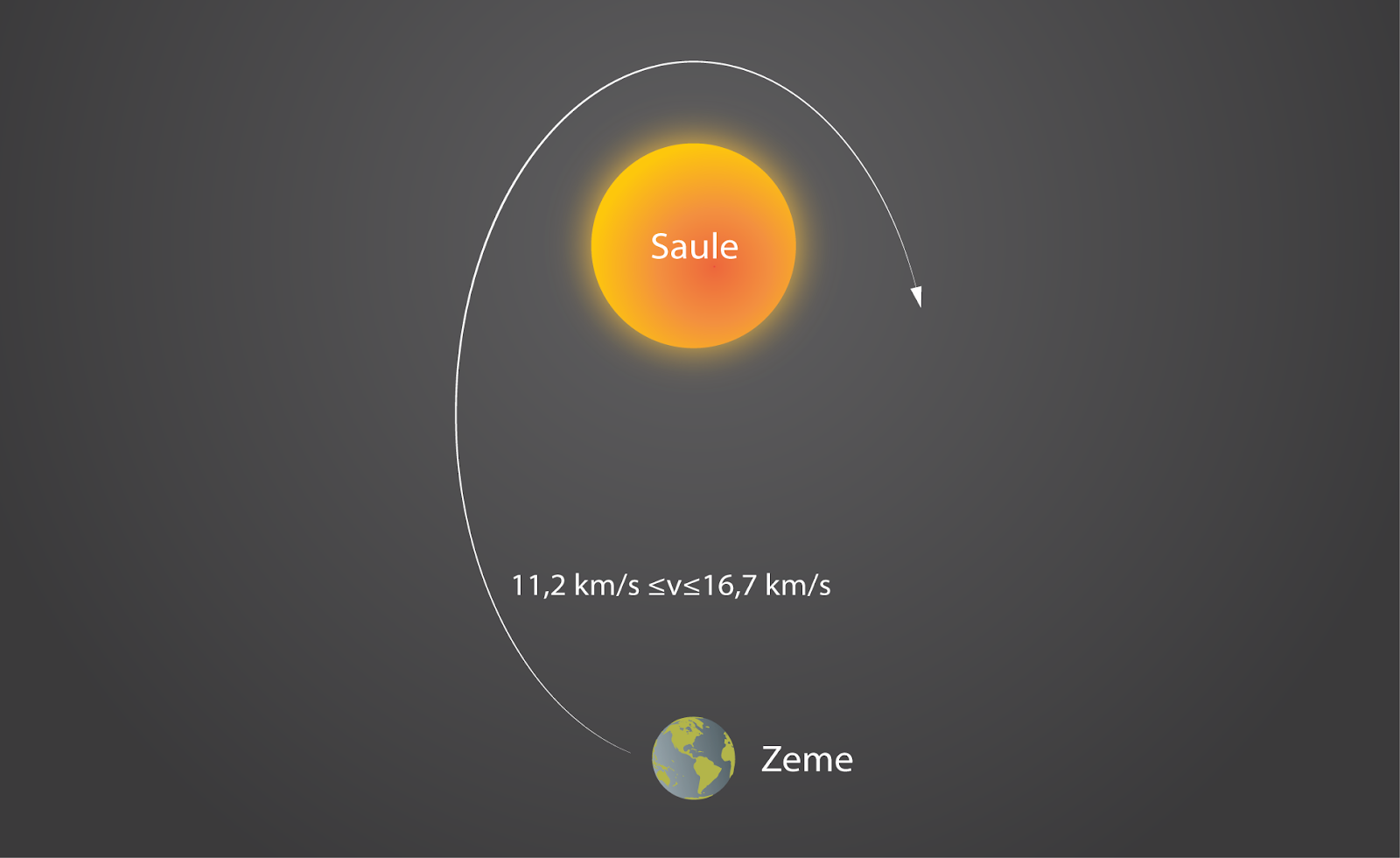
4. att. Otrā kosmiskā ātruma pārsniegšana
Lai pavadonis izbēgtu arī no Saules gravitācijas spēka, tad tam ir jāpiešķir trešais kosmiskais ātrums v=16.7 km/s. Iegūstot šādu ātrumu, pavadonis lido virzienā prom no Saules sistēmas. 1977. gadā tika palaisti divi kosmiskie aparāti Voyager-1 (5. att.) un Voyager-2, kuriem tika piešķirts trešais kosmiskais ātrums, lai tie lidotu prom no Saules sistēmas un piegādātu zinātnisku informāciju par lidojuma apstākļiem. 2012. gadā Voyager-1 sasniedza Saules sistēmas robežu.

5. att. Voyager-1
Uz pavadoni, kas riņķo ap Zemi, darbojas centrtieces spēks FC, kas izliec pavadoņa trajektoriju, tādā veidā nodrošinot tā orbītu (1. att.). Šādā gadījumā kā centrtieces spēks darbojas gravitācijas spēks FG, kas darbojas starp pavadoni uz Zemi. Centrtieces spēku var izteikt FC=maC=mv2/(R+h), kur
m - pavadoņa masa, kg
aC - centrtieces paātrinājums, m/s2
v - pavadoņa lineārais ātrums, m/s
R - Zemes rādiuss, m
h - pavadoņa augstums virs zemes, m
Gravitācijas spēku var izteikt FG=GMm/(R+h)2, kur
G - gravitācijas konstante
M - Zemes masa (M=6,0·1024 kg)
(R+h) - attālums starp Zemes centru un pavadoni, m
Tā kā centrtieces spēku nodrošina gravitācijas spēks, tad FC=FG un mv2/(R+h)=GMm/(R+h)2.
Tālāk iegūst v2=GM/(R+h).
Ja pavadonis kustas tuvu Zemes virsmai jeb h ir daudz mazāks par R, tad (R+h)≈R un v2=GM/R.
Atceroties (Fiztēma - Gravitācijas spēks un brīvās krišanas paātrinājums), ka brīvās krišanas paātrinājums g=GM/R2, iegūst v2=gR. Ievitojot brīvās krišanas paātrinājumu uz zemes virsmas uz Zemes rādiusu, iegūst lineārā ātruma vērtību v≈7,9 km/s, kas atbilst pirmajam kosmiskajam ātrumam.
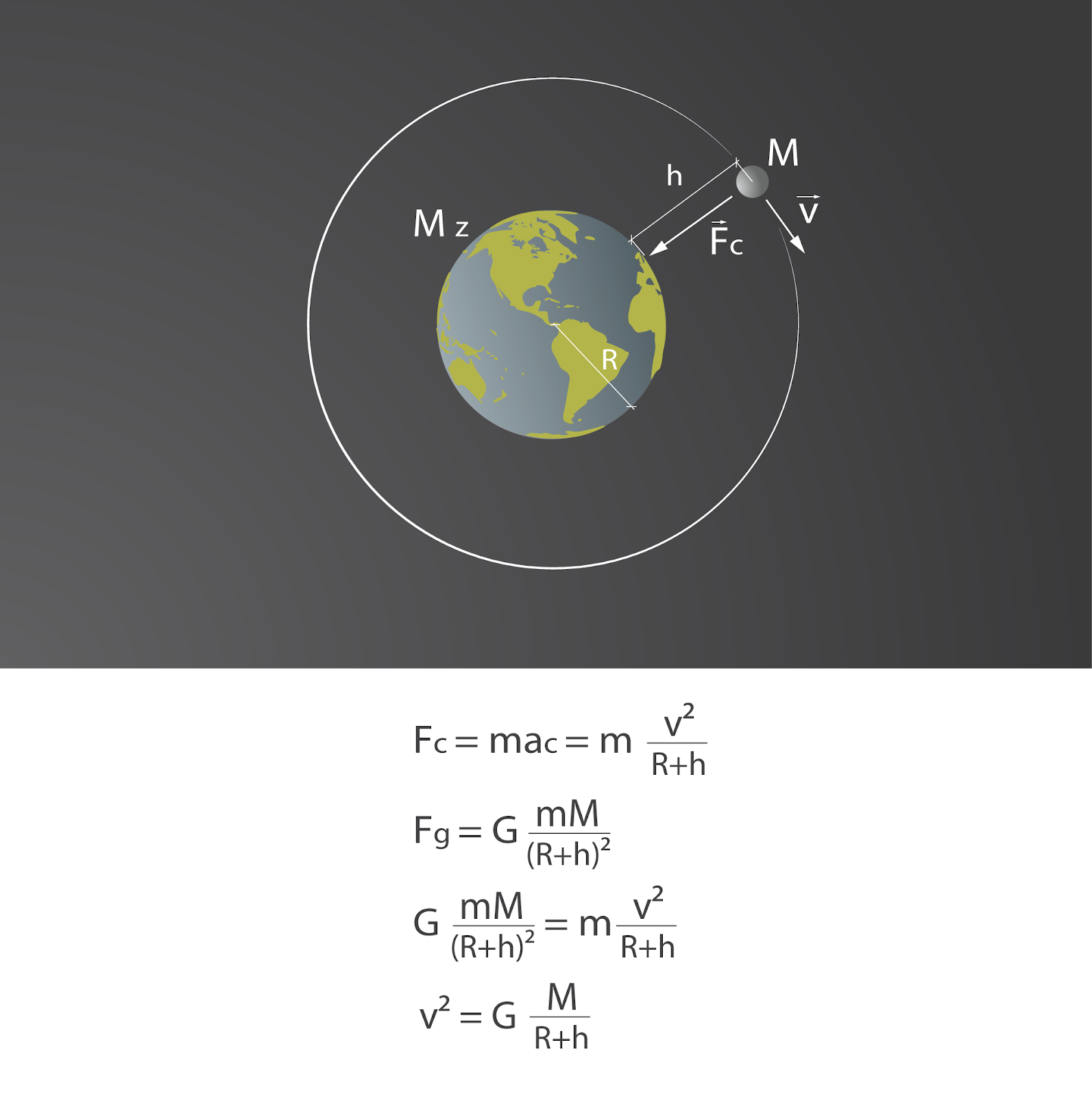
1. att. Gravitācijas spēks kā centrtieces spēks
Ja pavadoņi kustas dažādos augstumos virs Zemes (2. att.), to kustības ātrumi atšķiras. Apskatot iepriekš iegūto sakarību v2=GM/(R+h) redzams, ka kustības ātrums nav atkarīgs no pavadoņa masas, bet no attāluma līdz Zemes centram R+h. Līdz ar to ja viens pavadonis atrodas augstumā h1, otrs augstumā h2 un h2>h1, tad, salīdzinot pavadoņu kustības ātrumu, v1>v2. Tas nozīmē, ka jo tuvāk zemes virsmai atrodas pavadonis, jo ātrāk tas kustas.
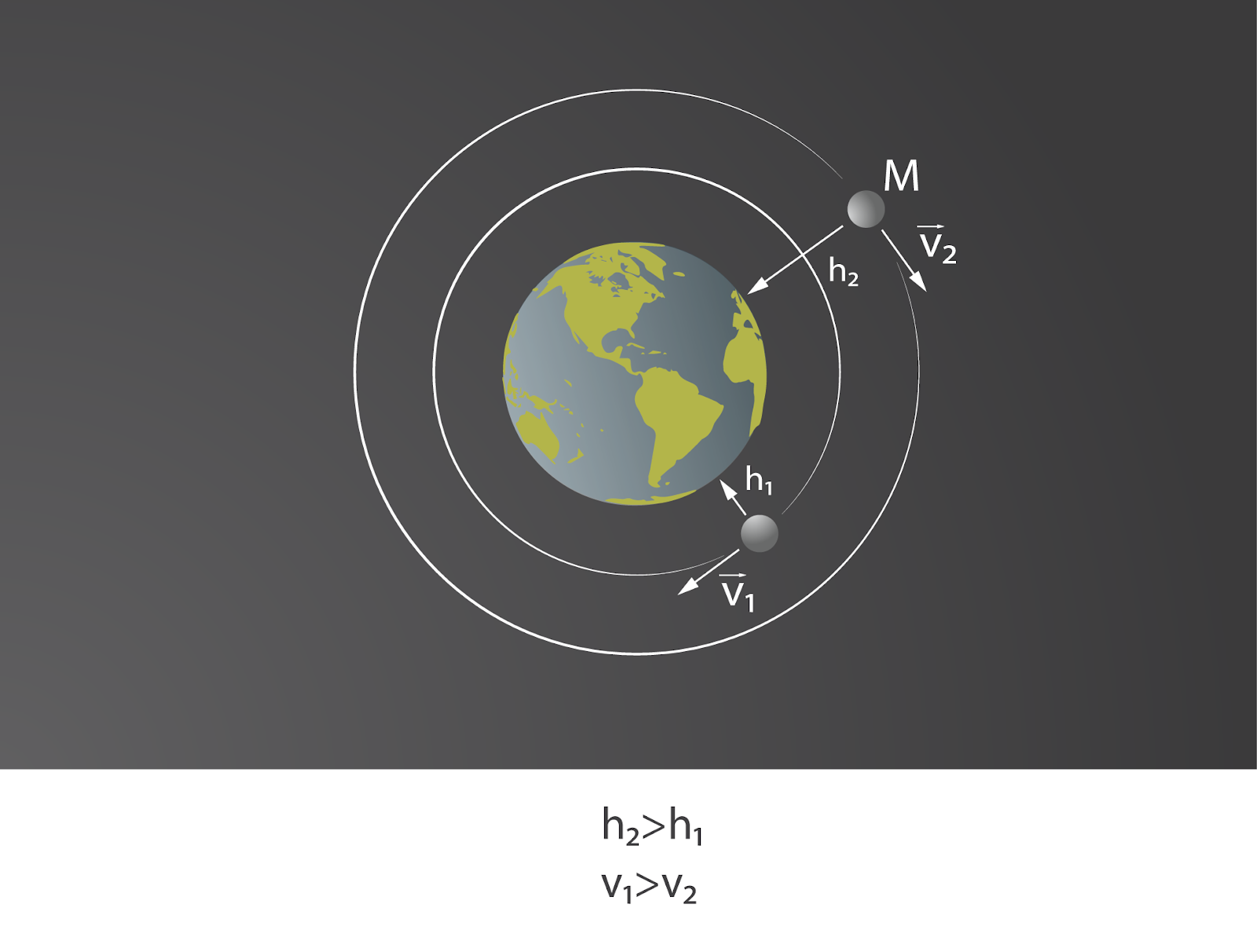
2. att. Pavadoņu kustības ātrumi dažādās orbītās
Lai kosmiskā zonde iegūtu pietiekamu ātrumu nokļūšanai uz tālākām Saules sistēmas vietām, izdevīgi izmantot citu planētu gravitācijas spēku, kas var darboties līdzīgi katapultai. 1997. gadā uz Saturnu tika palaista kosmiskā zonde Cassini, kuras kustības trajektorija redzama 3. att. Nokļūšanai mērķi, tika izmantots gan Zemes un Veneras, gan arī Jupitera gravitācijas spēks.
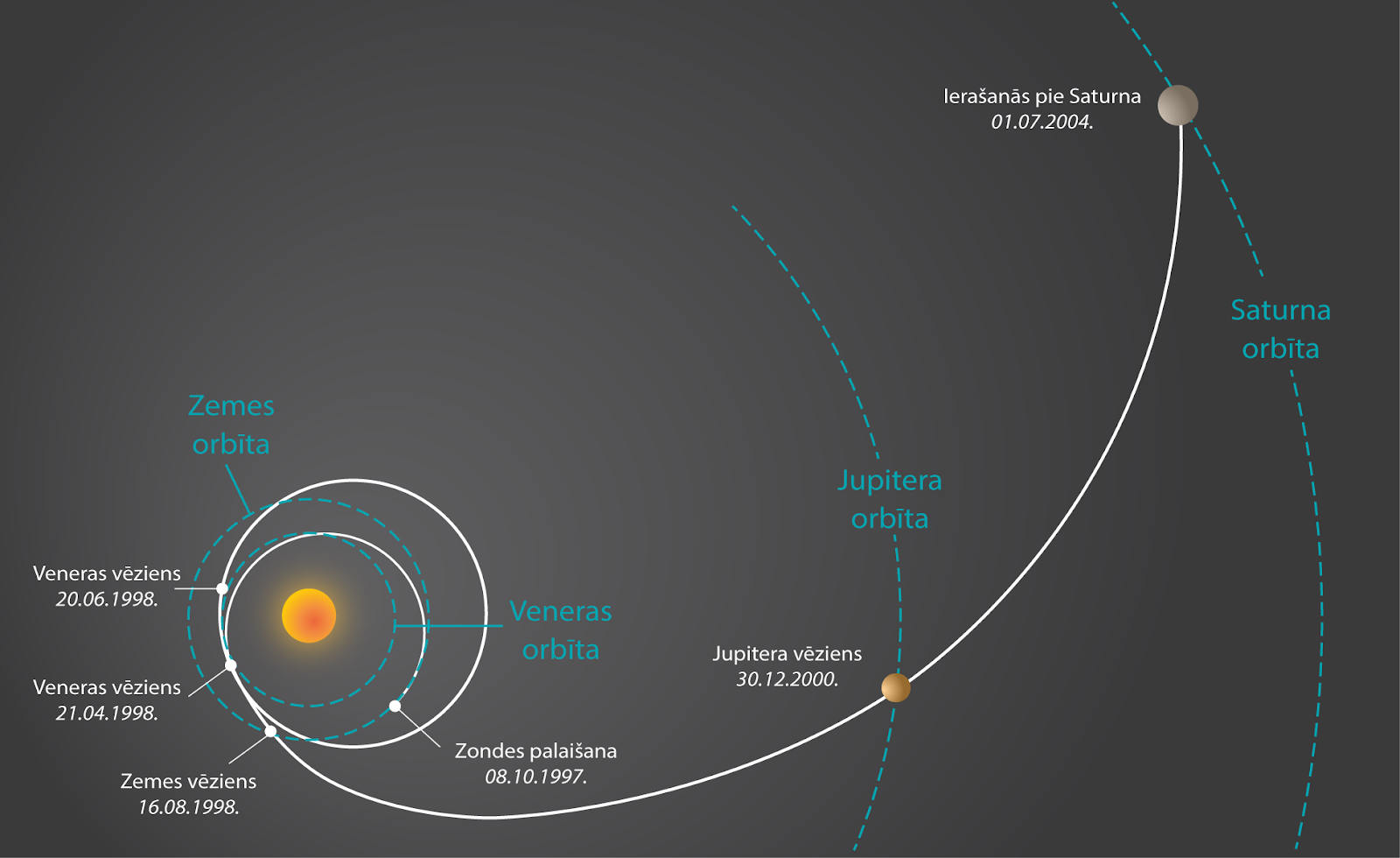
3. att. Kosmiskās zondes ceļš uz Saturnu