Katram cietam ķermenim ir noteikta forma. Ja uz šo ķermeni iedarbojamies ar kādu spēku, tad mēs varam to deformēt jeb izmainīt tā formu. Par deformāciju sauc ķermeņa formas un tilpuma maiņu. Tomēr ķermenim “patīk” sava forma, tādēļ notiek pretošanās formas izmaiņai. Spēku, ar kādu ķermenis pretojas deformācijām, sauc par elastības spēku Fe (1. att. a). Elastības spēks ir elektromagnētiskās mijiedarbības izraisīts spēks, kas darbojas starp ķermeni veidojošajiem atomiem (1. att. b). Nedeformētam ķermenim elektromagnētiskie spēki ir līdzsvarā, savukārt tad, kad mēs cenšamies ķermeni deformēt, zūd līdzsvars starp šiem spēkiem un tā rezultātas rodas elastības spēks. Situācija ir līdzīga ja mēs deformētu ķermeni, kas sastāv no ar atsperēm savienotām bumbiņām. Saspiežot ķermeni tiek saspiestas atsperes, kas pretojās deformācijai ar savu elastības spēku (1. att. c)
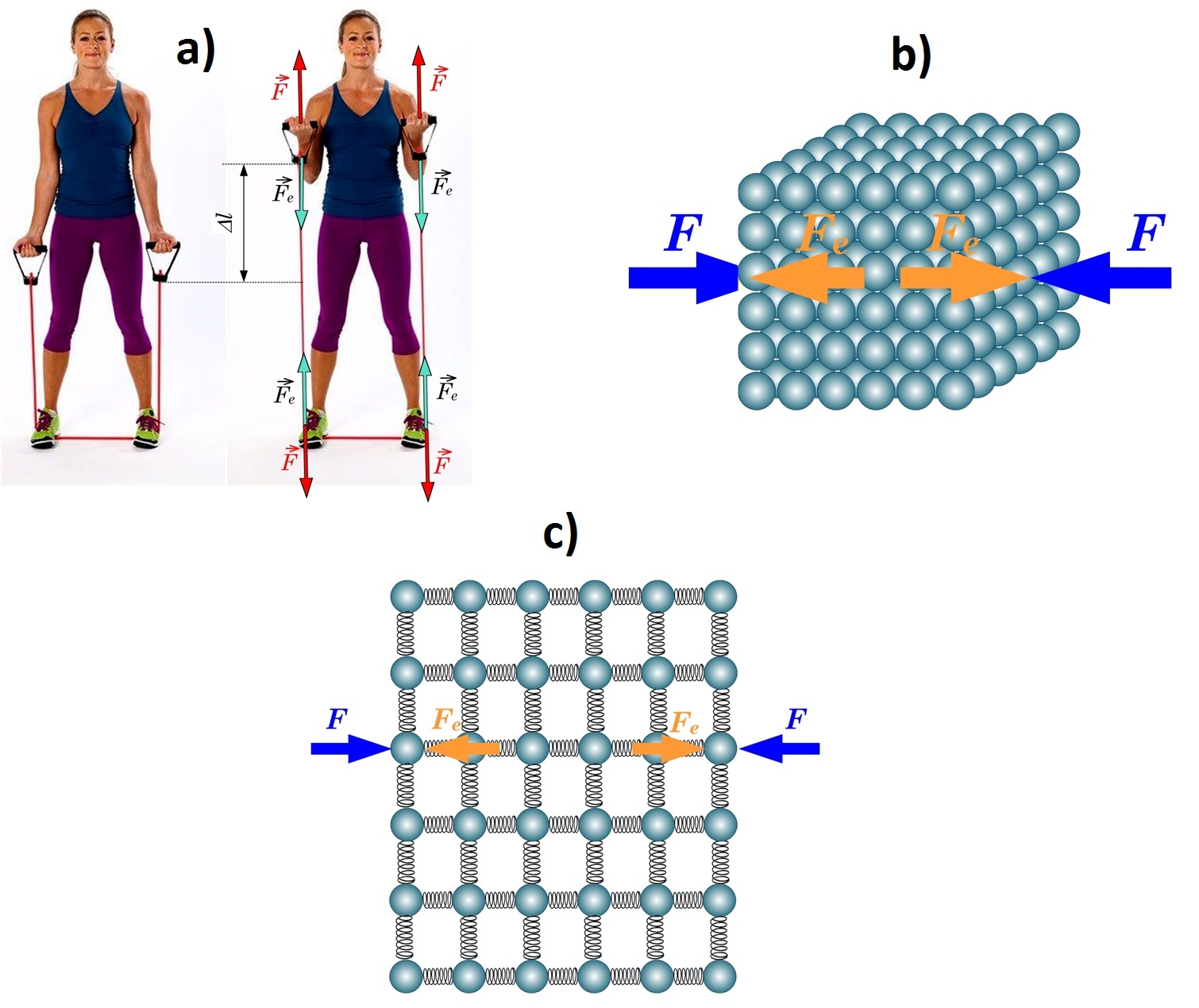
1. att. Ķermeņa deformēšana
Ņemot vērā deformācijas spēka izraisītas izmaiņas ķermeņa formā, ķermeni var deformēt vai nu elastīgi vai plastiski. Par elastīgo jeb atgriezenisko deformācija runā tad, ja pēc deformējošā spēka noņemšanas ķermenis atgūst savu iepriekšējo formu, kas bija pirms deformēšanas sākšanas, piemēram, rakete pirms un pēc sadursmes ar bumbiņu (2. att. a). Ja pēc deformējošā spēka noņemšanas ķermenis pilnībā savu formu neatgūst, tad saka, ka ķermenis ir bijis pakļauts plastiskajai deformācijai (2. att. b). Ja deformējot tiek pārsniegta ķermeņa izturības robeža, tad ķermenis sagrūst!
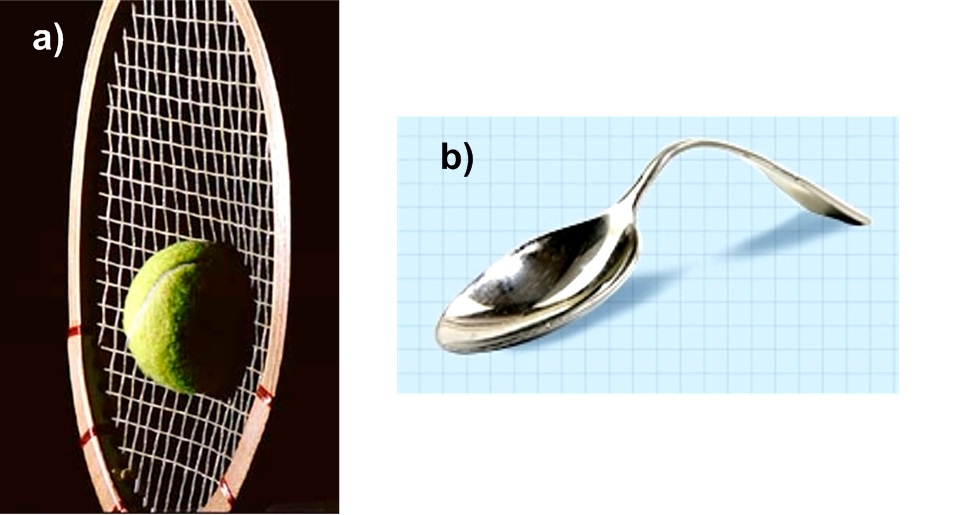
2. att. Elastīga un plastiska deformācija
Elastīgas deformācijas gadījumā spēku, ar kādu ķermenis pretojās deformācijām, var izteikt kā Fe=k·∆x, kur
k - elastības koeficients vai stinguma koeficients (atsperēm), N/m
∆x - pagarinājums, m
Šo elastības spēka izteiksmi sauc par Huka likumu un tas norāda, ka elastības spēks elatīgās jeb atgriezeniskās deformācijās ir tieši proporcionāls pagarinājumam (3. att. a). Ja uzzīmē grafiku elastības spēka atkarībai no pagarinājuma, tad Huka likuma izpildīšanas gadījumā šis grafiks ir taisne (3. att. b).
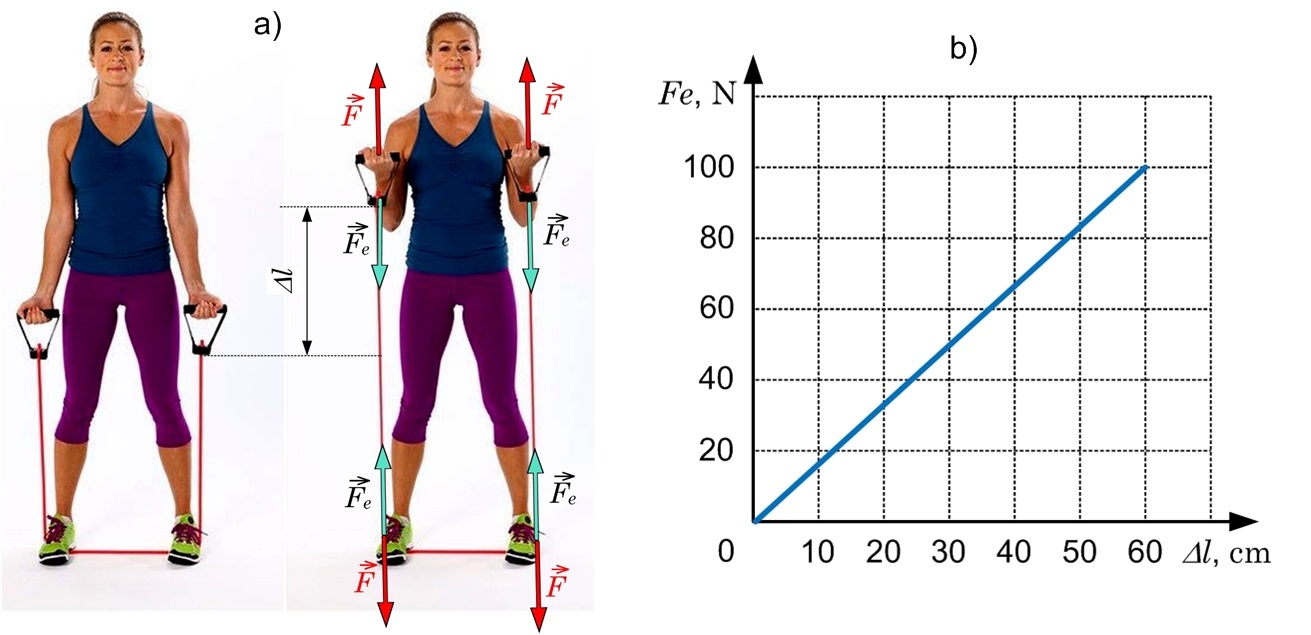
3. att. Huka likums
Elastības koeficientu k (4. att.) ir atkarīgs no ķermeņa formas un tā veidojošā materiāla: k=E·S/l0, kur
E - Junga modulis, Pa
l0 - ķermeņa sākotnējais garums, m
S - šķērsgriezuma laukums, m2
Junga modulis raksturo materiāla elastības īpašības neatkarīgi no tā kāds ķermenis no tā ir izveidots.
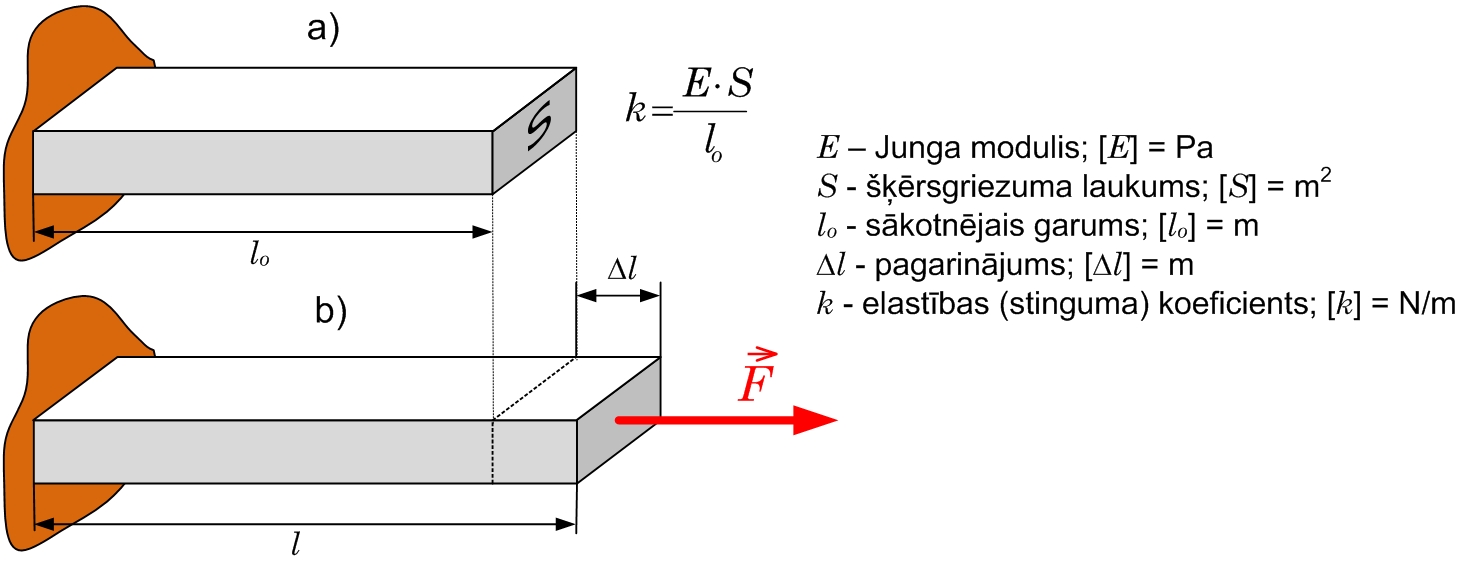
4. att Elastības koeficienta veidotāji
5. att. redzams dažādu materiālu Junga moduļu salīdzinājums. Jo lielāks ir Junga modulis, jo grūtāk materiāls pakļaujas deformācijai, piemēram, gumijai E=7 MPa, tādēļ gumiju ir viegli deformēt, bet dzelzim E=200 000 MPa, līdz ar to šo materiālu ir 28570 reizes grūtāk deformēt nekā gumiju.
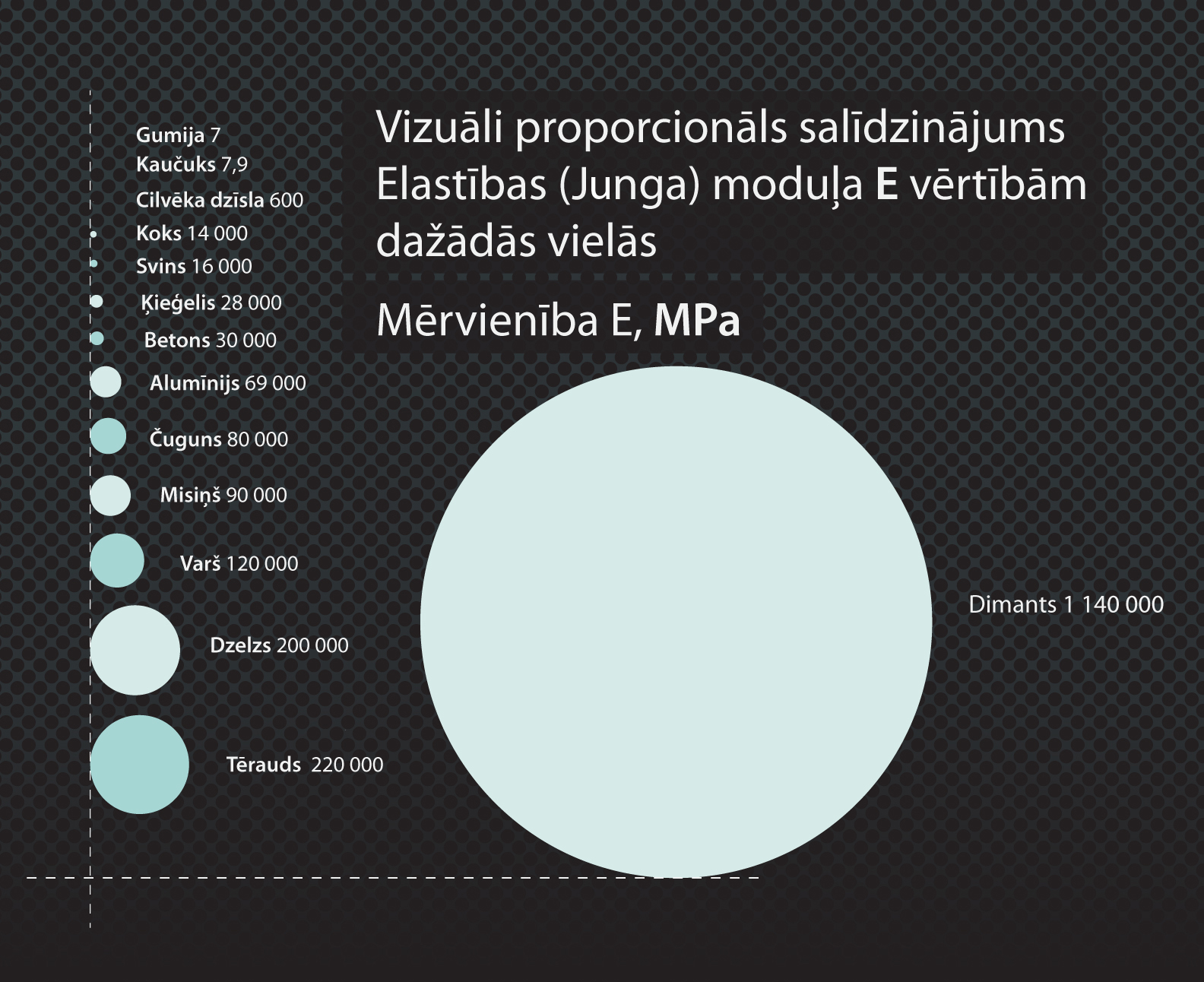
5. att Dažādu materiālu Junga moduļa vērtības
Deformācijas spēka izraisīto efektu var raksturo ar spriegumu σ=F/S, ko iegūst pielikto spēku izdalot ar šķērsgriezuma laukumu, uz kuru spēks darbojas. Katram materiālam ir maksimālais spriegums, ko tas var izturēt, un tas ir labs mērs lai novērtētu vai attiecīgo materiālu var lietot kārotajam mērķim vai nē. Ja sprieguma atkarību no deformācijas attēlo grafiski (1. att.), tad var paredzēt materiālu uzvedību pie dažādu deformāciju lieluma. Pie mazām deformācijām grafiks ir taisne un šajā brīdī materiāls tiek elastīgi deformēts. Tālāk seko plastiskā deformācijas posms, kas nozīmē paliekošas deformācijas materiālā. Visbeidzot grafiks pārtrūkst brīdī, kad tiek sasniegta izturības robeža un materiāls sabrūk. (1. att.).

1. att Sprieguma atkarība no deformācijas
Deformācijas atšķiras ne tikai pēc lieluma, bet arī pēc veida. Ja deformācijas rezultātā ķermenis tiek pagarināts, tad to sauc par stiepi (2. att. a). Stiepei ir pakļautas dažādas troses, ķēdes, mūzikas instrumentu stīgas vai, piemēram, griestu lampas iekare (2. att. a). Ja ķermenis tiek deformēts tā, ka tā garums samazinās, tad to sauc par spiedi (2. att. b). Spiedei pakļautas dažādas virsmas, ēkus sienas un pamati, galda kājas un ēkus kolonas (2. att. b).
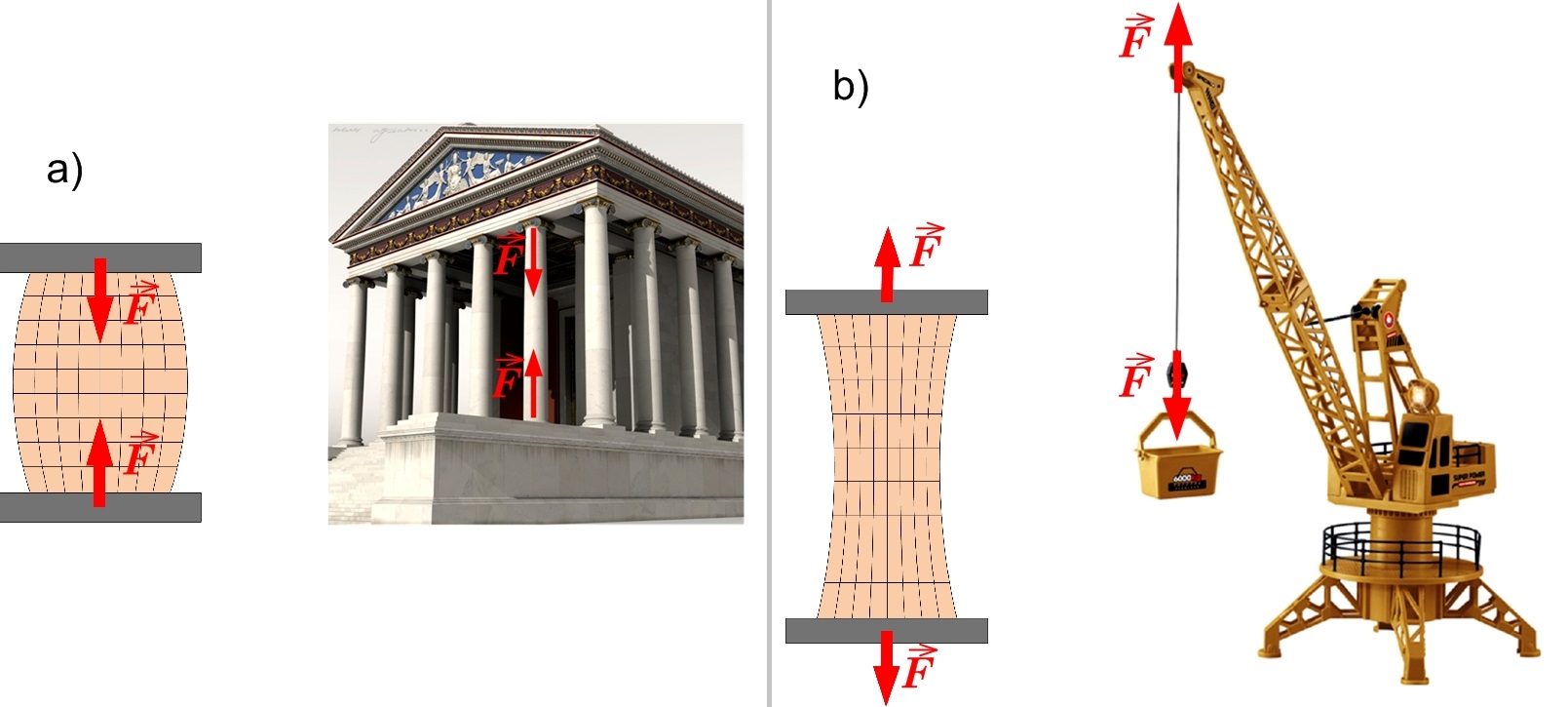
2. att Stiepes un spiedes deformācijas
Ja deformācijā apvienojas gan stiepe, gan spiede, tad to sauc par lieci. Ja ķermenis ir pakļauts liecei, tad vienā pusē ķermenim notiek spiedes deformācija, bet otrā stiepes. Līdz ar to sanāk, ka pa vidu ir deformācijai nepakļauts (neitrāls) slānītis (3. att. a). Šim neitrālajam slānītim ir maza nozīmē ķermeņa izturībā, tādēļ konstrukcijas, kas pakļautas lieces deformācijai, var veidot ar mazāk materiālu vidusslāni vai vispār tukšu vidu (3. att. b), tādā veidā ietaupot materiālu.
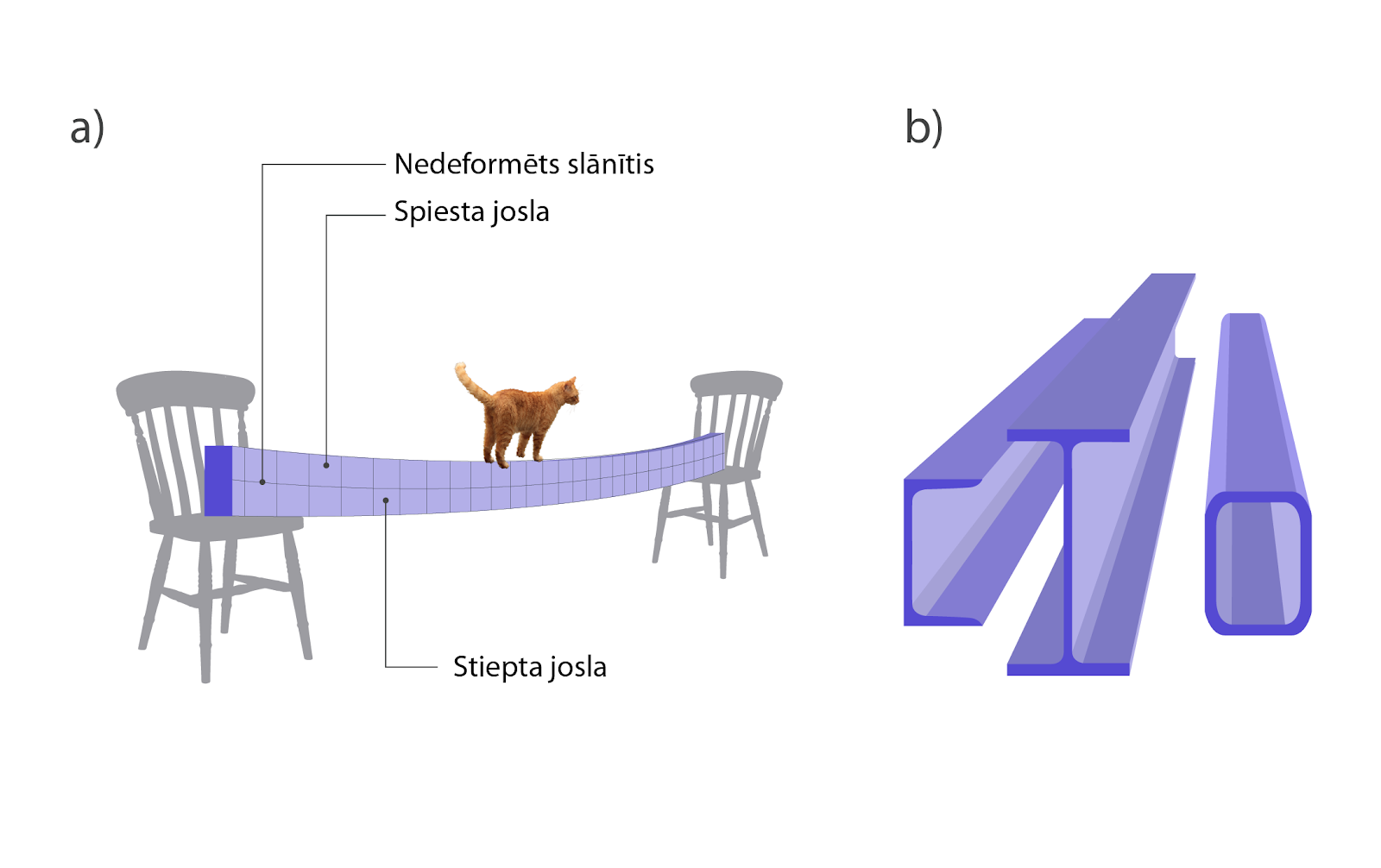
3. att Lieces deformācija
Deformāciju, kurā savstarpēji nobīdās vielas slāņi, sauc par bīdi (4. att. a). Bīdei tiek pakļauts materiāls, ja to žāgē (4. att. b), kā ārī bīde ir atbildīga par dažādu lietu, piemēram, apģērbu, apavu (4. att. c) un darbarīku nodilšanu.
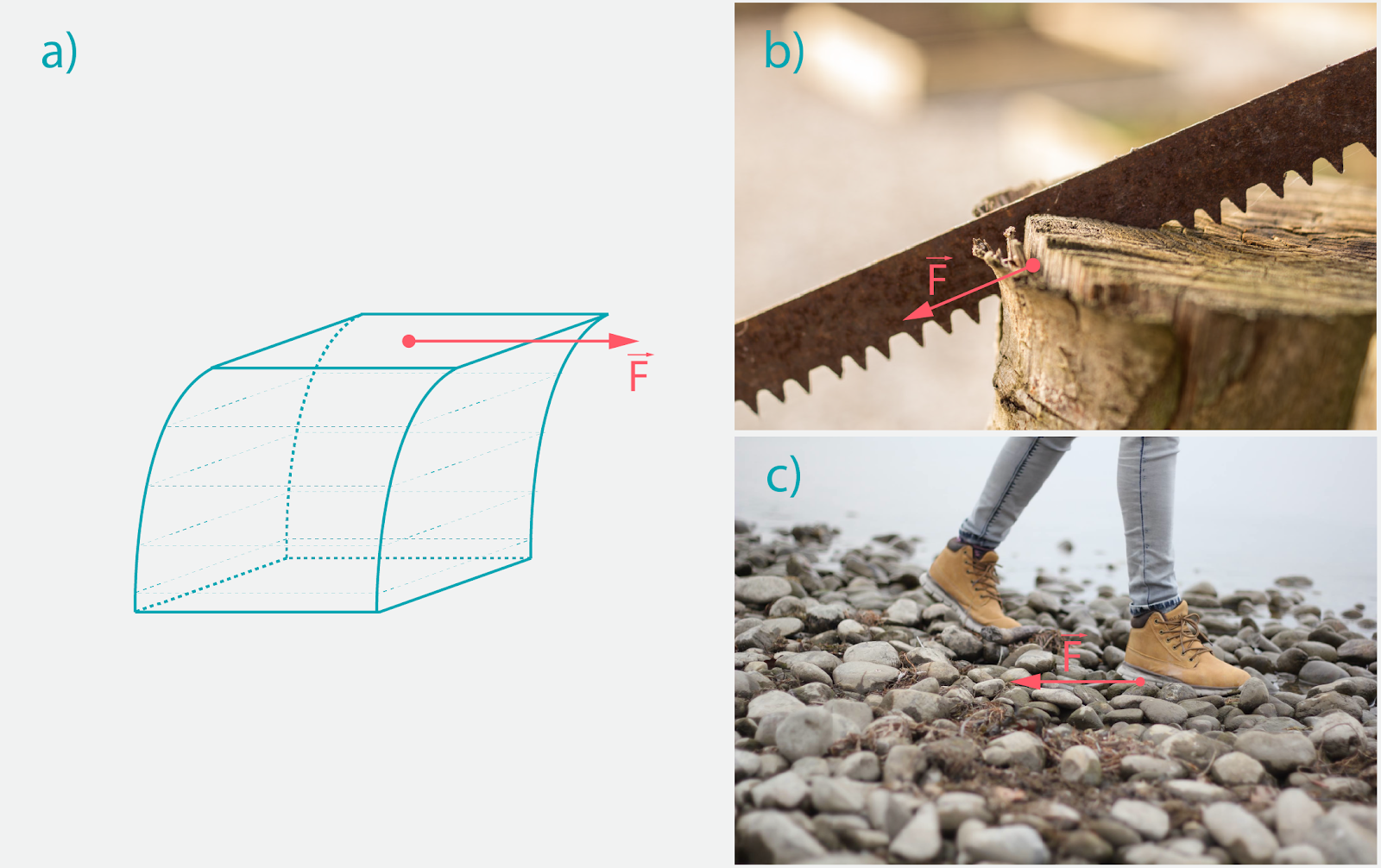
4. att Bīdes deformācija
Vērpes deformācijā ķermenis tiek savērpts jeb vērpē darbojas divi pretējos virzienos pielikti spēki (5. att. a), kas darbojas vērpšanas asij perpendikulārā plaknē. Šādā deformācija sastopama vietās, kur notiek kāda rotācijas kustība, piemēram, izmantojot skrūvgriezi (5. att. b), urbjot, pievelkot skrūves vai pagriežot aizdedzes atslēgu.
FIZMIX video par dažādām deformācijām
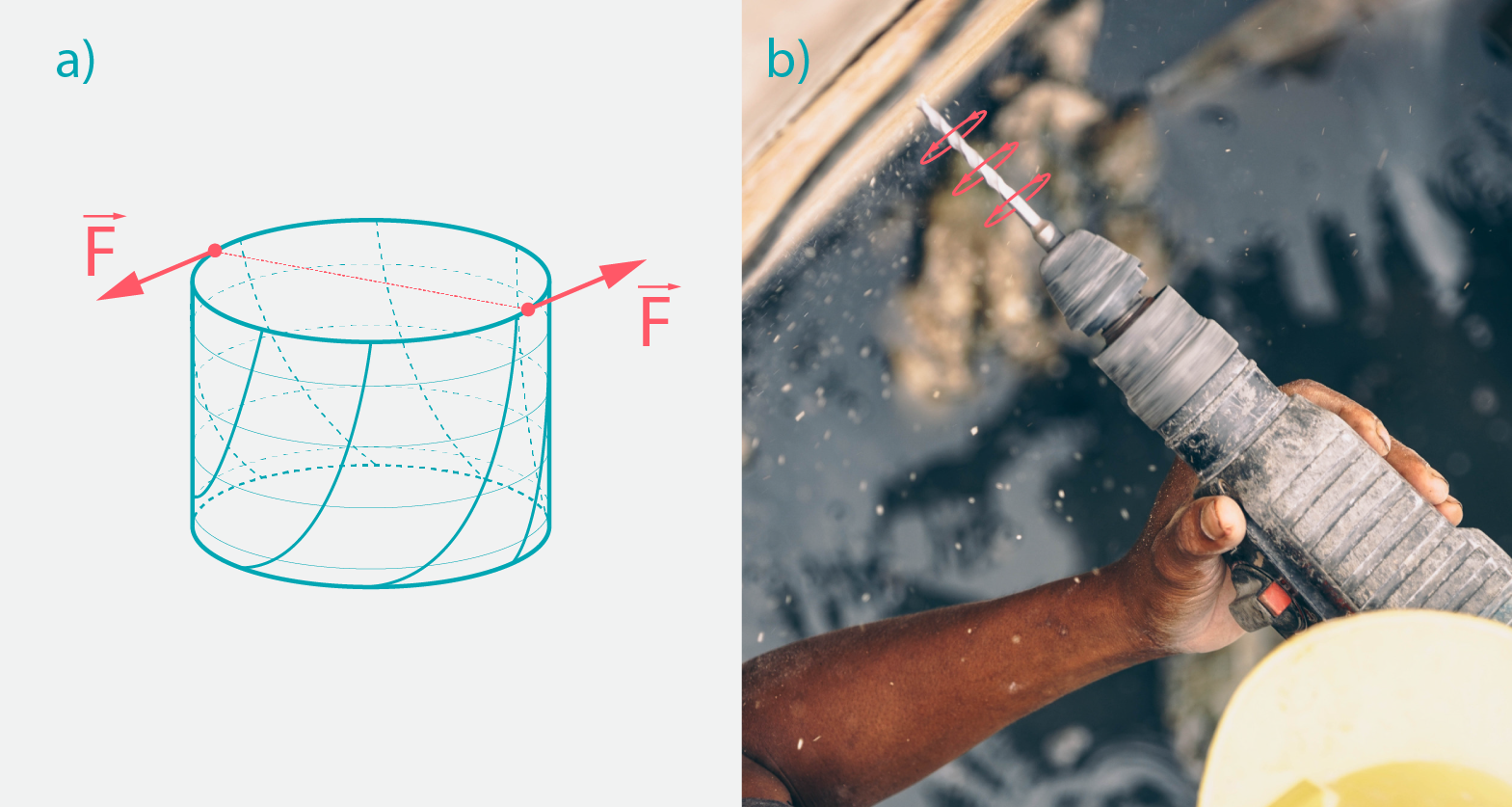
5. att Vērpes deformācija
Līdz ar elastīgu deformāciju, ķermenī uzkrājas arī deformācijas potenciālā enerģija, ko var aprēķināt, izmantojot izteiksmi Ep=k·∆x2/2, kur
k - elastības koeficients, N/m
∆x - deformācija, m
Pēc izteiksmes var redzēt, ka, pieaugot deformācijai, uzkrāta enerģija pieaug kvadrātiski (6. att.).
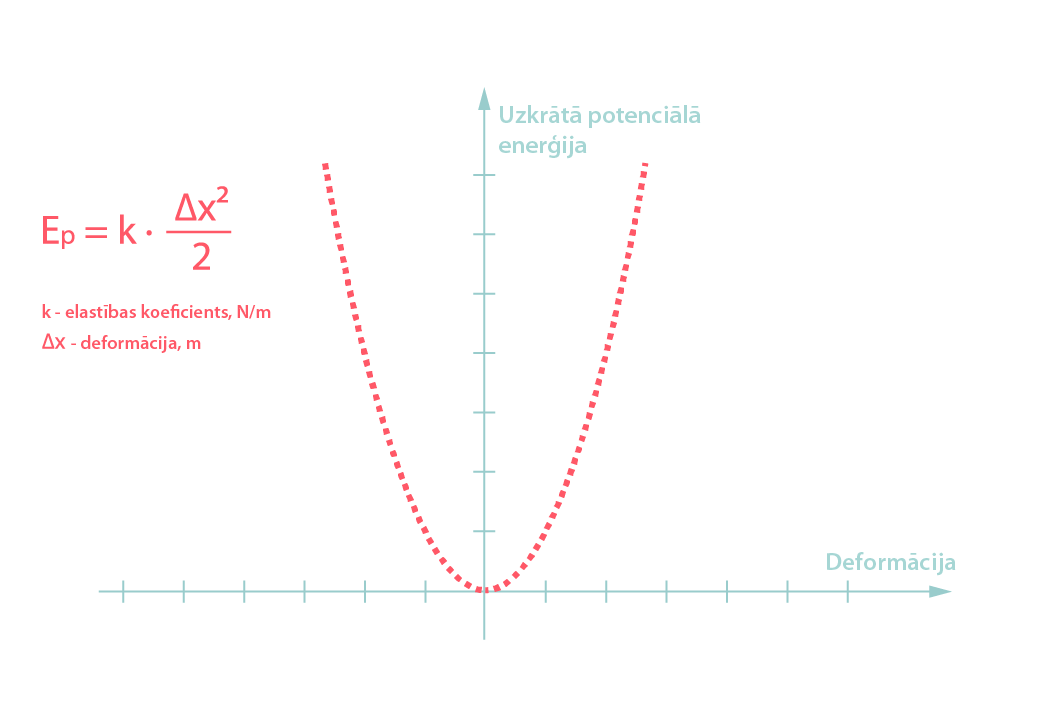
6. att Deformācijas potenciālā enerģija
Pirmajā solī tika apskatīta elastības spēka izteiksme k=E·S/l0. Šīs izteiksmes izpildīšanos var uzskatāmi parādīt eksperimentā. Ja abas puses pareizina ar pagarinājumu ∆x, tad iegūst k·∆x=E·S·∆x/l0 jeb Fe=E·S·∆x/l0. Izsakot pagarinājumu, iegūst ∆x=Fe·l0/(E·S). No šīs izteiksmes seko, ka iekarinot divu vienādu materiālu stieņos, kuriem ir vienāds sākuma garums l0, vienu un to pašu atsvaru (lai rastos vienāds elastība spēks), stienim ar mazāko šķērsgriezuma laukumu (1. att. a) ir jādeformējas vairāk nekā stienim ar lielāku šķērsgriezuma laukumu (1. att. b).
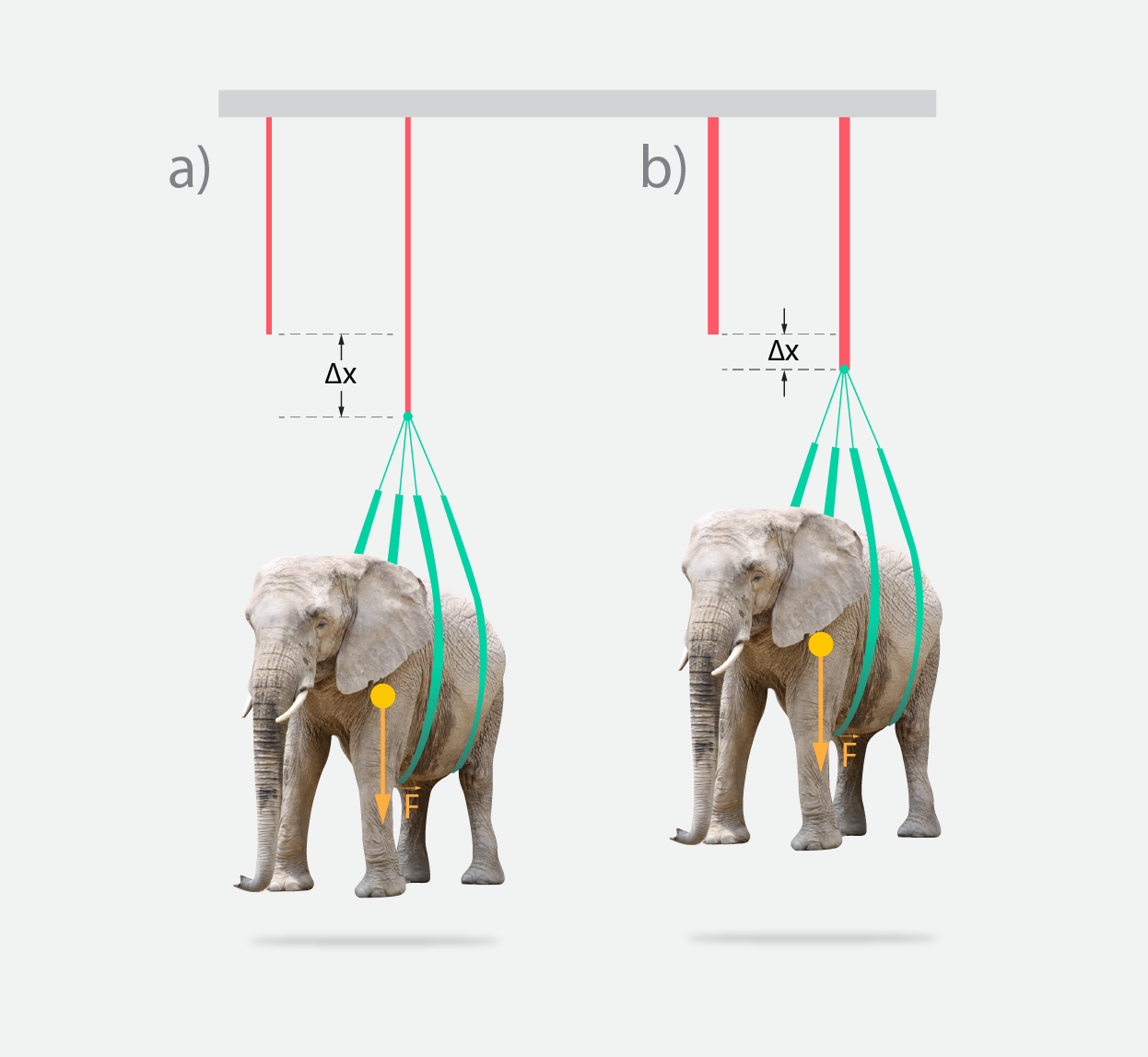
1. att Deformācijas atkarība no šķērsgriezuma laukuma
Ja eksperimentu atkārto ar diviem vienāda materiāla un šķērsgriezuma stieņiem, bet ar atšķirīgu sākuma garumu, tad vienādas masas atsvars īsāko stieni (2. att. a) deformēs mazāk nekā garāko (2. att. b).
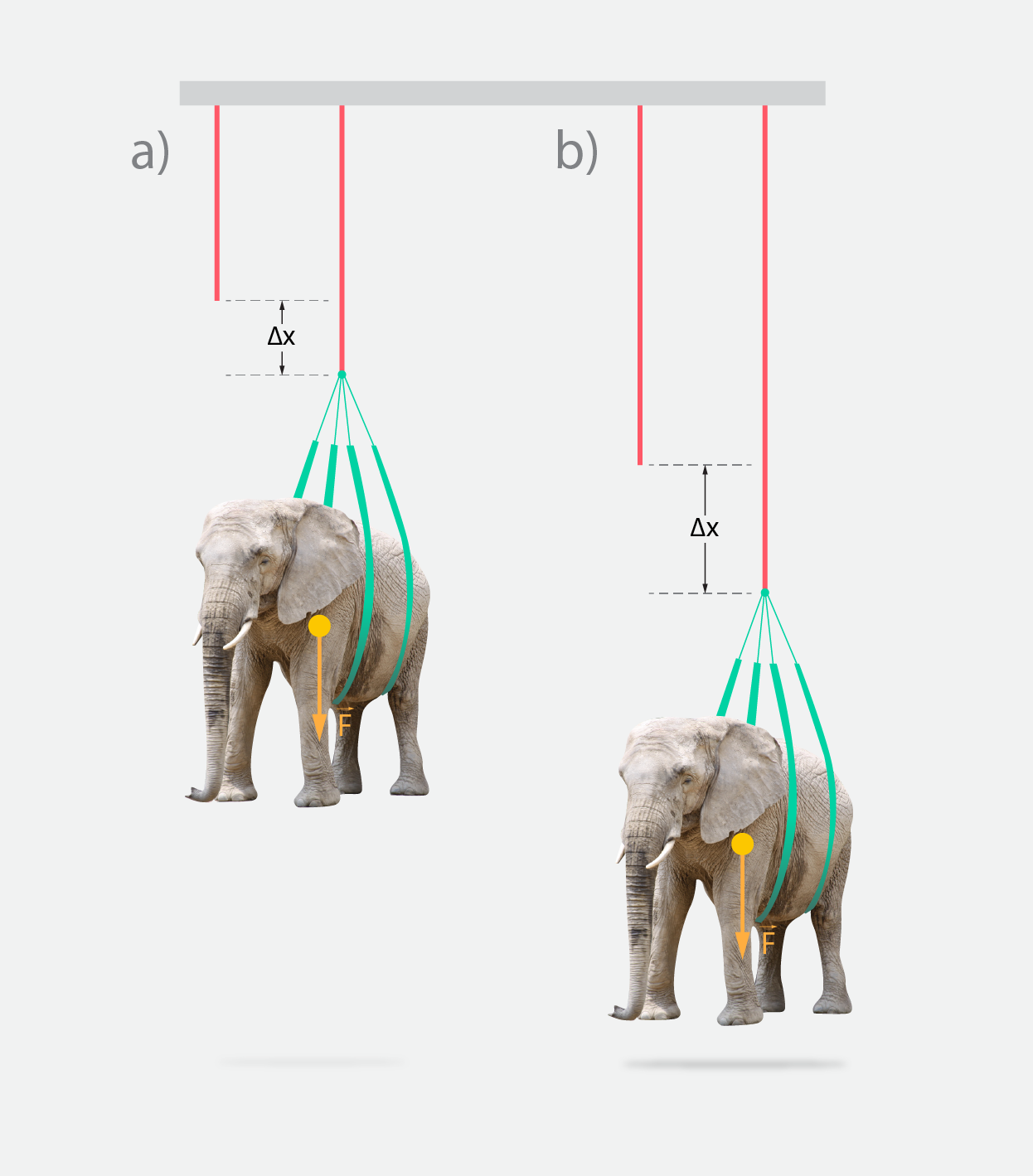
2. att Deformācijas atkarība no sākuma garuma
Lietojot dažādas lietas un ierīces, kas tiek deformētas, mēs parasti izvairamies no to sagraušanas, jo tas var būt kaitīgi veselībai, tādēļ ir svarīgi novērtēt, cik lielu spēku var izturēt attiecīgs objekts vai konstrukcija. 2. solī tika apskatīts grafiks sprieguma atkarībai no deformācijas, kurā atradās arī sagraušanas punkts. Dažādi materiāli deformējot uzvedās dažādi (3. att.), tādēļ ja gribam zināt konkrēta materiāla elastības robežu vai maksimāl pieļaujamo slodzi, ir jāveic šī materiāla izpēte vai jāizmanto jau iegūti dati, pirms šo materiālu lietojam kāda konstrukcijā. Nepareiza materiālu izvēle vai slodžu sadale var rezultātos lielās traģēdijās.
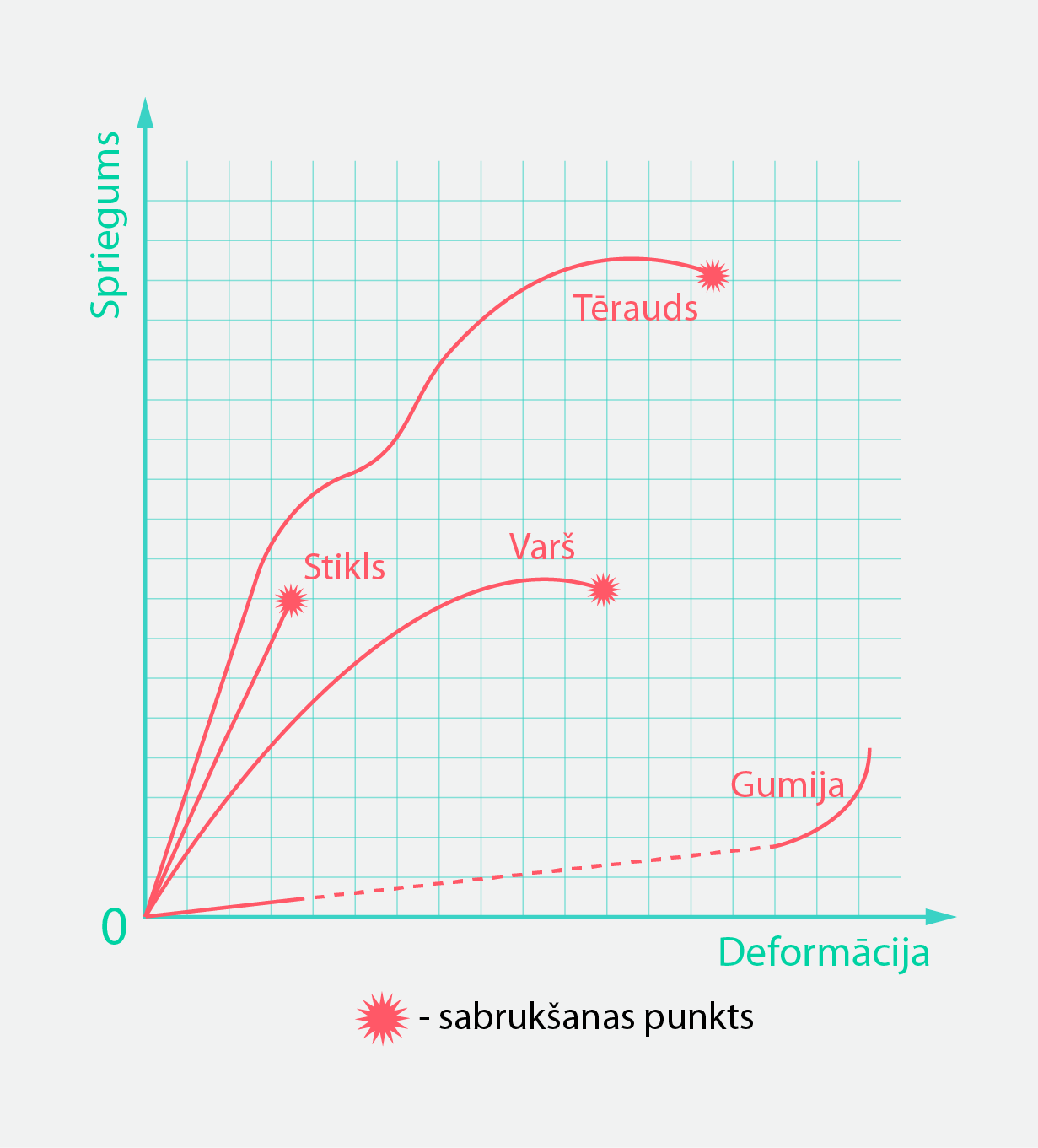
3. att Dažādu materiālu sprieguma atkarība no deformācijas