Spēki un mijiedarbība

Uzdevumu atrisinājums pieejams video formātā un rakstiski.

Jebkura ķermeņa kustību apraksta II Ņūtona likums \(\overrightarrow{F}=m\overrightarrow{a}\), kur \(\overrightarrow{F}\)- kopspēks, kas darbojas uz ķermeni, un \(\overrightarrow{a}\) - ķermeņa paātrinājums. Mūsu uzdevumā ķermenis  ir planēta. Vienīgais spēks, kas darbojas uz planētu, ir gravitācijas pievilkšanās spēks starp planētu un Sauli, kas arī piešķir planētai centrtieces paātrinājumu. Tādā gadījumā II Ņūtona likuma vektoriālo formulu var uzrakstīt "moduļos": \(F=ma\).

Gravitācijas spēka formula: \(F=G\frac{m_1 m_2}{R^2}\), kur (mūsu piemērā) \(m_1=M\) ir Saules masa; \(m_2=m\) - planētas masa; \(R\) - attālums starp Sauli un planētu.

Centrtieces paātrinājuma formula:  \(a=\frac{v^2}{R}\), kur \(v\) - planētas kustības lineārais ātrums par orbītu ap Sauli.

Ievietojot abas formulas II Ņūtona likuma sakarībā, iegūsim: \(G\frac{Mm}{R^2}=m\frac{v^2}{R}\) 

Saīsināsim \(R\) un \(m\) un izteiksim planētas kustības lineāro ātrumu: \(v=\sqrt{\frac{GM}{R}}\)

No iegūtās formulas var secināt, ka planētas kustības lineārais ātrums ir apgriezti proporcionāls kvadrātsaknei no tās attāluma līdz Saulei: ja \(R\uparrow\), tad \(v\downarrow\) (un otrādi). Ja Zemes orbītas rādiuss ir lielāks, nekā Venēras orbītas rādiuss, tad Zemes lineārais ātrums ir mazāks, nekā Venēras lineārais ātrums.

Vai otrādi, ja Venēras orbītas rādiuss ir mazāks, nekā Zemes orbītas rādiuss, tad Venēras lineārais ātrums ir lielāks, nekā Zemes lineārais ātrums.

Atbilde: Venēras kustības lineārais ātrums pa orbītu ap Sauli ir lielāks, nekā Zemes kustības lineārais ātrums.

Uzdevuma izpilde eksāmenā - 32%. 

Vērtēšanas kritēriji

Izmanto gravitācijas likumu, 2. Ņūtona likumu un centrtieces paātrinājuma izteiksmi - 1 punkts.

Iegūst sakarību, kas apraksta lineāro ātrumu - 1 punkts

Pamatojot ar iegūto sakarību, izdara korektu secinājumu par Venēras un Zemes lineārā kustības ātruma savstarpējo saistību - 1 punkts

Piezīmes: 

Ja izteiksme \(v=\sqrt{G\frac{M}{R}}\)ir iegūta, neizmantojot 2. Ņūtona likumu, gravitācijas likumu un centrtieces paātrinājuma formulu, risinājums tiek vērtēts ar 0 punktiem.

Ja ir sniegta atbilde par planētas kustības lineāro ātrumu, skaidrojumā neizmantojot 2. Ņūtona likumu, gravitācijas likumu un centrtieces paātrinājuma formulu, risinājums tiek vērtēts ar 0 punktiem.

Skolēnu risinājumu un to vērtējumu piemēri

1. piemērs: risinājums ir novērtēts ar 3 punktiem. 

2. piemērs: risinājums ir novērtēts ar 3 punktiem. 

3. piemērs: risinājums ir novērtēts ar 2 punktiem (skolēns nav atbildējis uz jautājumu par Zemi un Venēru). 

4. piemērs: risinājums ir novērtēts ar 1 punktu (par 2. Ņūtona likuma, gravitācijas likuma un centrtieces paātrinājuma izteiksmes izmantošanu)

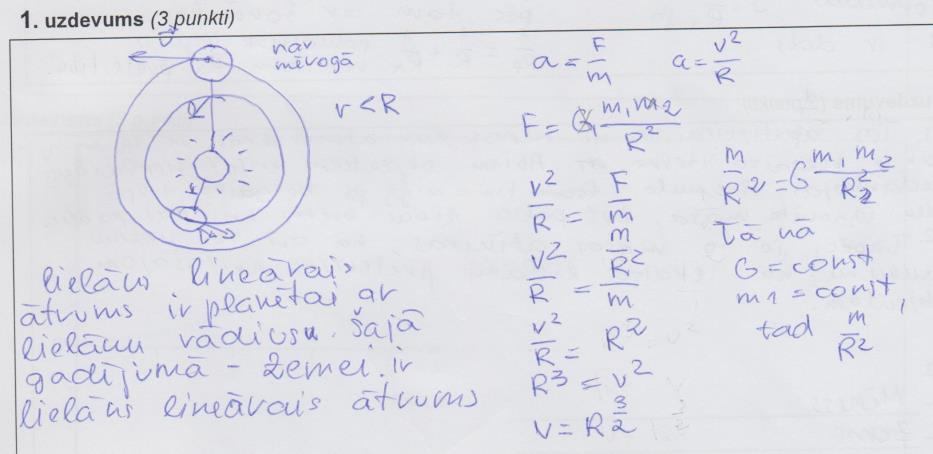
5. piemērs: risinājums ir novērtēts ar 0 punktiem (autora spriedumi nav pamatoti ar fizikas likumiem).